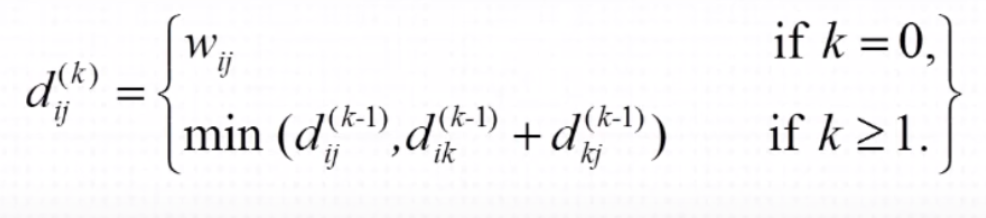최단 경로

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

Floyd-Warshall Algorithm

1. Floyd-Warshall Algorithm

• Floyd-Warshall Algorithm은 모든 최단 경로를 구하는 방법
• 다익스트라 알고리즘은 음의 가중치에서는 사용 못하나 이것은 가능
• optimal substructure의 개념을 이용하여 최단 경로를 찾는다.
• optimal substructure란 특정 경로 안에 무수히 많은 경로가 있을 때, 중간 정점들이 각각 최단이 된다면 이를 모두 이은 경로 또한 최단이 된다는 개념이다.

2. 기본 로직

• 2개의 테이블을 사용
• 모든 경로에 대한 비용을 저장하는 테이블 (예시로 D라고 부름)
• 각 정점까지 가기 직전의 정점을 저장한 테이블 (예시로 P라고 부름)
• D와 P에는 처음엔 인접 리스트에 대한 내용만 들어가 있음
• 그 후 경로를 추가 할 때마다 두 테이블이 갱신
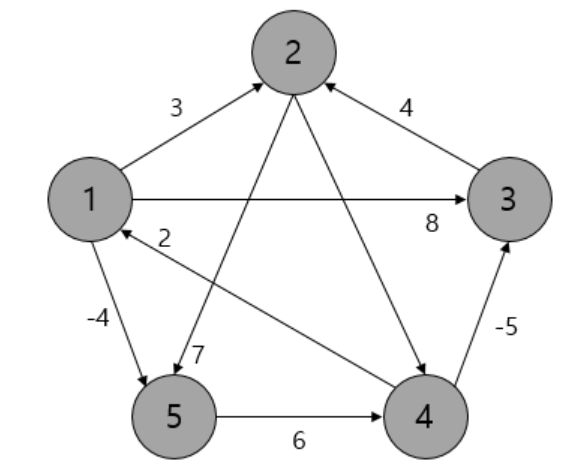
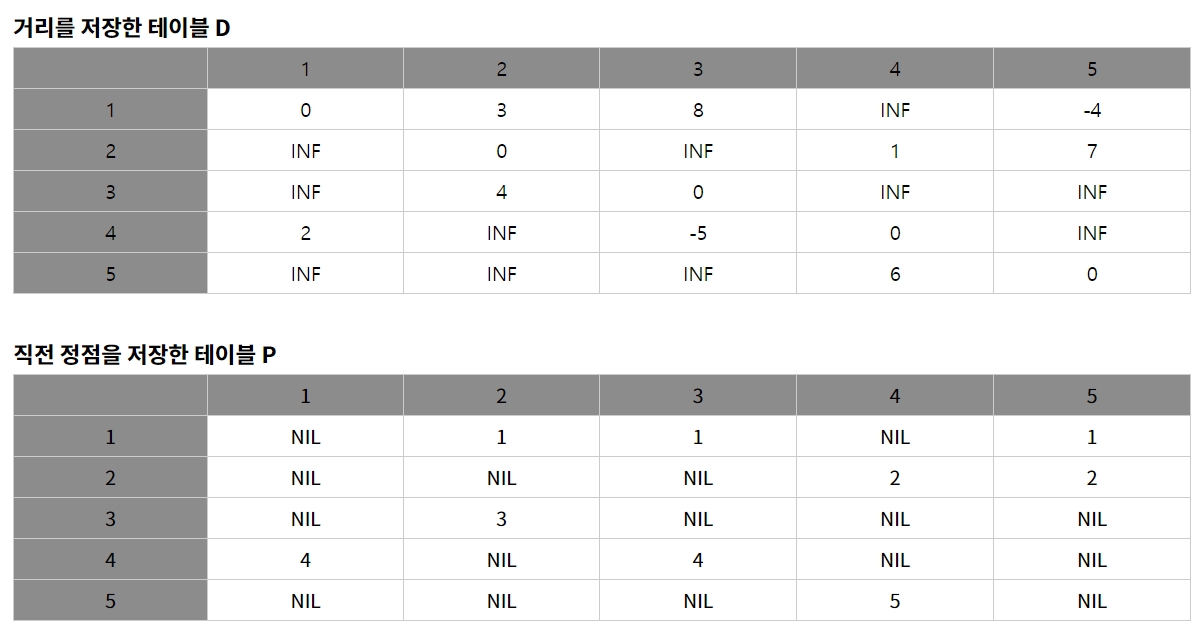
• 아래는 예제 그래프와 최초 D와 P에 대한 그림
• INF(NIL)는 무한대를 의미. 직전 정점이 없다. 즉, 연결이 없다라는 뜻.

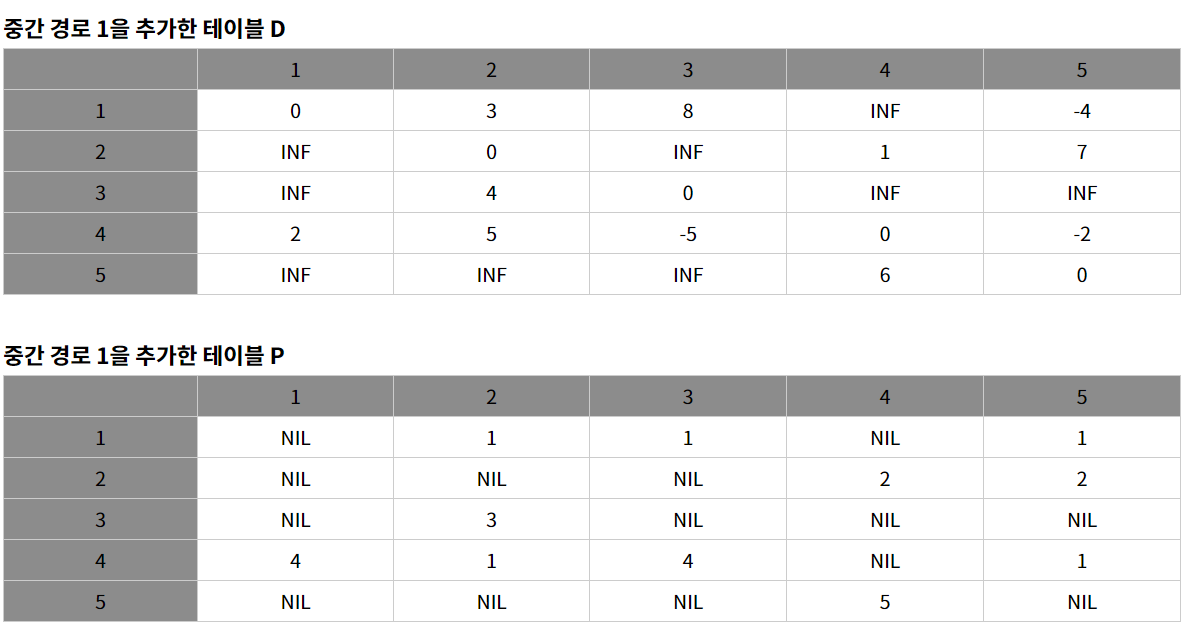
2.1 중간 경로 1을 추가한 후

• 경로 1을 중간 경로로 하는 테이블을 구한다.
• 4 -> 2가 중간경로 1을 추가하면 4->1->2로 접근 할 수 있고, 4->5도 4->1->5로 접근 할 수 있게 됨
• 그러면 아래와 같이 갱신된다.
• 이를 반복

3. 수식 & Pseudo Code

• dij^(k) 를 k 라는 정점을 이번에 추가하였을 때 i 정점부터 j 정점까지의 최단경로 라고 정의.
• 즉 k 라는 정점을 새로 추가하였을 때 i 정점부터 j 정점까지의 최단경로는 기존의 i 정점 부터 j 정점까지 이동했던 경로 와 i 정점부터 k 정점까지의 최단 경로 + k 정점부터 j 정점까징의 최단 경로 중 최소값.

• 시간 복잡도 O(n^3)

4. 경로 찾기 & 출력

5. 최종 결과 (예시)