최단 경로

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

Dijkstra의 알고리즘

1. Dijkstra의 알고리즘

• bellman ford 알고리즘의 단점을 해결하기 위해 나온 알고리즘
• 불필요한 relax를 줄이기 위함

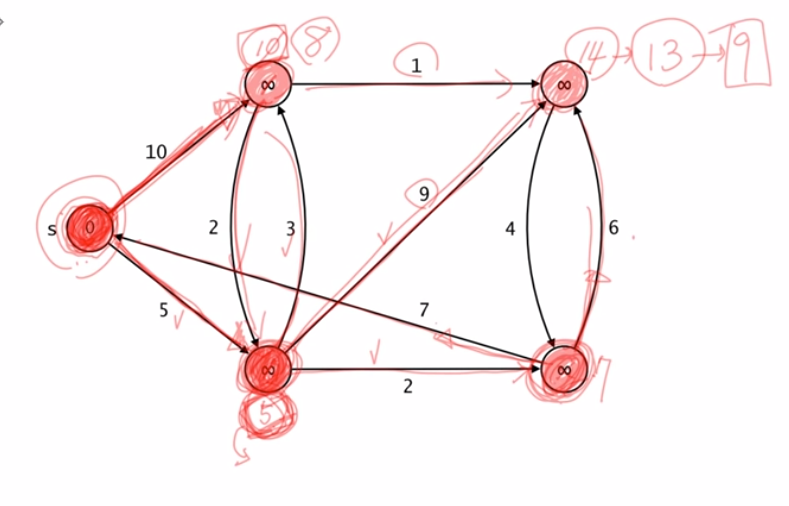
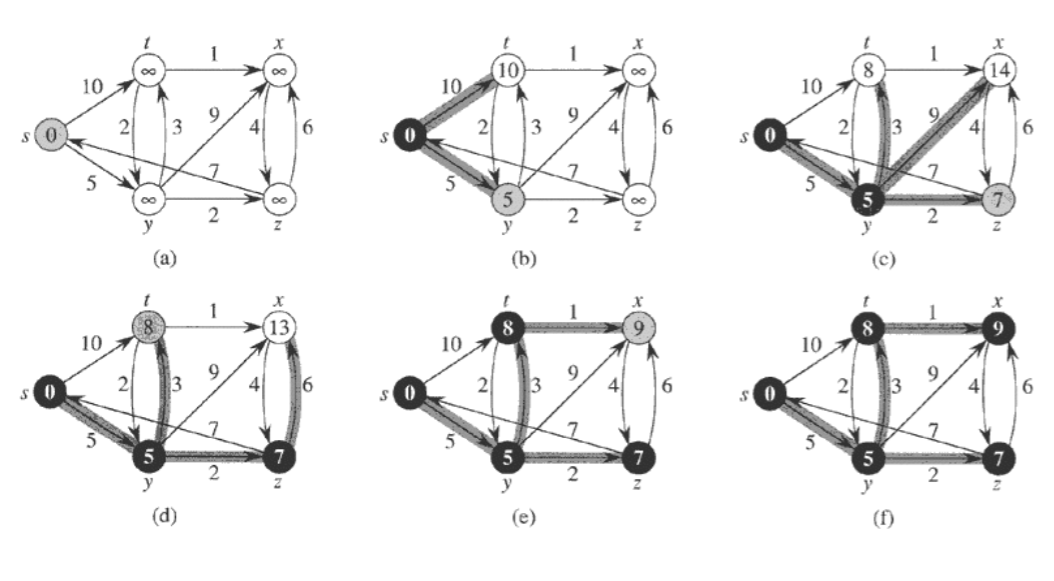
1.1 예시 그림

• 처음 시작 하는 노드를 S라고 하자

• S를 제외한 위의 그림에서 왼쪽 상단 노드를 A 기준으로 시계방향으로 A, B, C, D라고 하겠다.

• 각 노드들의 값들을 null처리

• 맨처음 S의 값은 0이다. 그리고 S를 TRUE(그림에서는 빨간색 칠하기) 처리 한다.

• S에서 시작하는 모든 엣지들에 대해서 연결된 노드들의 값을 relax한다.

• 그러면 A는 10이 되고 D는 5가 된다.

• 이때 TRUE가 된 S를 제외하고 나머지 노드들에 대해서 가장 작은 값인 D 노드를 기준으로 간다.

• D를 TRUE로 바꾸고 D에 연결된 노드들에 대해서 relax한다.

• 그러면 A는 8, B는 14, C는 7이 된다.

• 다시 TRUE를 제외한 A, B, C 중에서 가장 작은 값인 C를 기준으로 한다.

• C를 TRUE로 바꾸고 C에 연결된 노드들에 대해서 relax한다.

• 그러면 C는 13이 된다.

• 다시 TRUE를 제외한 A, B중 가장 작은 값인 A를 기준으로 한다.

• A를 TRUE로 바꾸고 relax한다.

• 그러면 B는 9가 된다.

1.2 Dijkstra 알고리즘 정리

• 음수 가중치가 없다고 가정
• s로부터의 최단경로의 길이를 이미 알아낸 노드들의 집합 S를 유지. 맨 처음엔 S={공집합}.
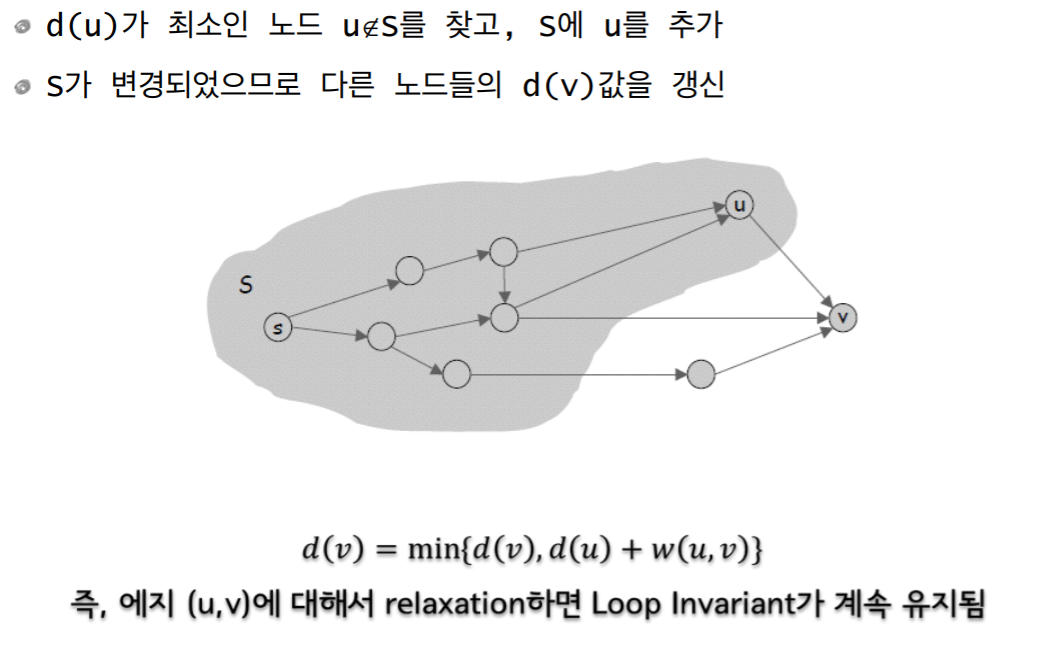
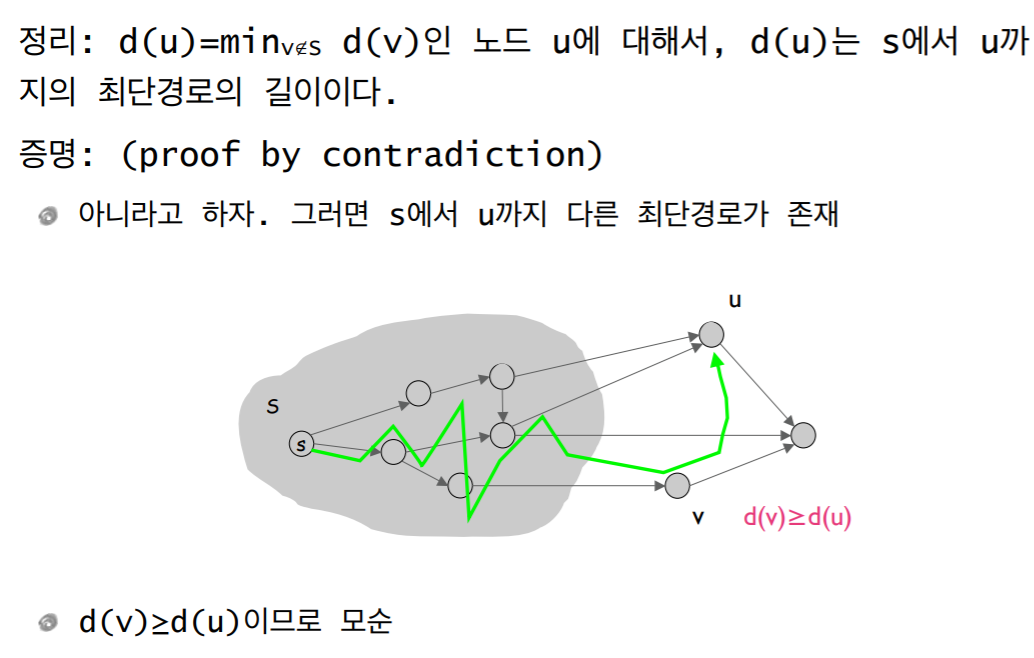
• Loop invariant:
  • u∉S인 각 노드 u에 대해서 d(u)는 이미 S에 속한 노드들만 거쳐서 s로부터 u까지 가는 최단경로의 길이

• 솔직히 이건 이해가 존나 안감. 알고리즘은 이해가 가는데 정의하는게 이해가 안가네 시발…

• u가 S에 속해졌으면 {u, v}에 대해서 relaxt해야 한다.
• 그러면 loop invariant가 유지된다.

1.3 Pseudo Code

• 5번 째 줄 S는 S가 있는게 아니라 공집합으로 되어야 한다.
• 1번 째 줄. 초기화 for 반복
• 집합 S가 총 노드의 개수보다 작으면 반복. S란 relax가 끝난 노드들의 집합
• 8번 째 줄. 집합 S에 속하지 않는 노드들에서 가장 작은 노드를 찾음
• 10번 째 줄. 그 노드에 대해서 relax
• 따라서 전체 노드들을 한번씩 도는 n-1번 반복 * 각 노드에 대해서 relax N번
• 시간복잡도는 O(N^2)이다.

1.4 시간복잡도

• Prim의 알고리즘과 동일함
• d 최솟값을 찾을 때 우선순위 큐를 사용하지 않고 단순하게 구현할 경우 O(n^2)
• 이진힙을 우선순위 큐로 사용할 경우 O(nlog2n + mlog2n)
• Fibonacci Heap을 사용하면 O(nlog2n+m)에 구현가능