감 1도 없는 개발자

감 1도 없는 개발자

여행을 꿈꾸는 개발자

최단 경로

Updated:

강의 사이트
  • http://www.kocw.net/home/search/kemView.do?kemId=1148815

최단경로

1. 최단경로

  • 가중치 (방향) 그래프 G=(V,E), 즉 모든 에지에 가중치가 있음
  • (무방향 그래프는 방향그래프랑 같다고 보면 됨. 양쪽으로 지나갈 수 있기에)
  • 경로 p=(v0,v1,…,vk)의 길이는 경로상의 모든 에지의 가중치의 합
  • 노드 u에서 v까지의 최단경로의 길이를 델타(u, v)라고 표시하자.

2. 유형

  1. Single-source: (one to all)
    • 하나의 출발 노드 s로부터 다른 모든 노드까지의 최단 경로를 찾아라.
    • 예: Dijkstra(다익스트라)의 알고리즘
  2. Single-destination: (one to all)
    • 모든 노드로부터 하나의 목적지 노드까지의 최단 경로를 찾아라.
    • Single-source 문제와 동일
    • 거꾸로 생각하면 single-source와 같다.
  3. Single-pair: (one to one)
    • 주어진 하나의 출발 노드 s로 부터 하나의 목적지 노드 t까지의 최단 경로를 찾아라
    • 최악의 경우 시간복잡도에서 Single-source 문제보다 나은 알고리즘이 없음
    • single-source를 구하다가 목적지가 t인 경로였다면 끝. 그래서 별게 없다.
  4. All-pairs: (all to all)
    • 모든 노드 쌍에 대해서 최단 경로를 찾아라.
    • floyd

3. 음수 가중치

  • 가중치는 보통 거리, 비용을 의미하므로 보통은 음수가 없다고 가정
  • 그러나 알고리즘에 따라 음수 가중치가 있어도 가능. 아닐 수도 있고. 100%는 아니라는 얘기

4. 기본 특성

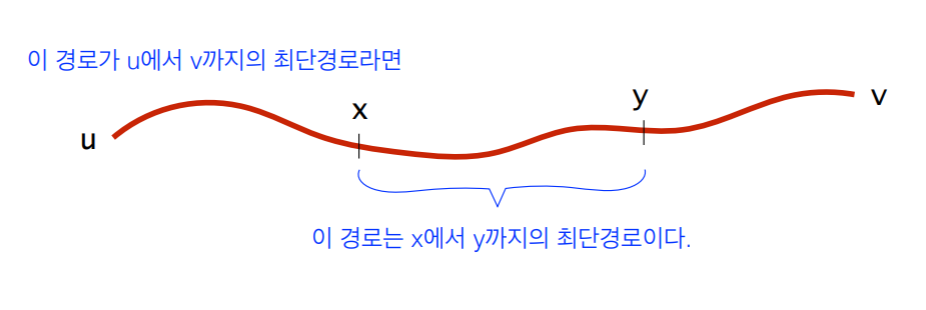
  • 최단 경로의 어떤 부분경로도 역시 최단 경로이다.

  • 최단 경로는 사이클을 포함하지 않는다. (음수 사이클이 없다는 가정하에서)

5. Single-source 최단경로 문제

  • 입력: 음수 사이클이 없는 가중치 방향그래프 G=(V,E)와 출발 노드 s∈V
  • 목적: 각 노드 v∈V에 대해서 다음을 계산한다.
    • d[v] : distance estimate(거리측정이라 부름)
      • 처음에는 d[s]=0, d[v]=∞로 시작한다.
      • 알고리즘이 진행됨에 따라서 d[v]는 감소해간다. 하지만 항상 d[v]≥δ(s,v)를 유지한다
      • 최종적으로는 d[v]=δ(s,v)가 된다.
      • 예를 들어 d[v] = 5라고 한다면 노드 s에서 v노드까지 거리가 5라는 이야기이다.
      • 꼭 direct가 아니고 여러 노드를 걸쳐서 총 합의 최솟값을 말하는 것이다.
      • 자세한 예는 6번을 보자
    • π[v]:
      • s에서 v까지의 최단경로상에서 v의 직전 노드(predecessor)
      • 그런 노드가 없는 경우 π[v]=NIL

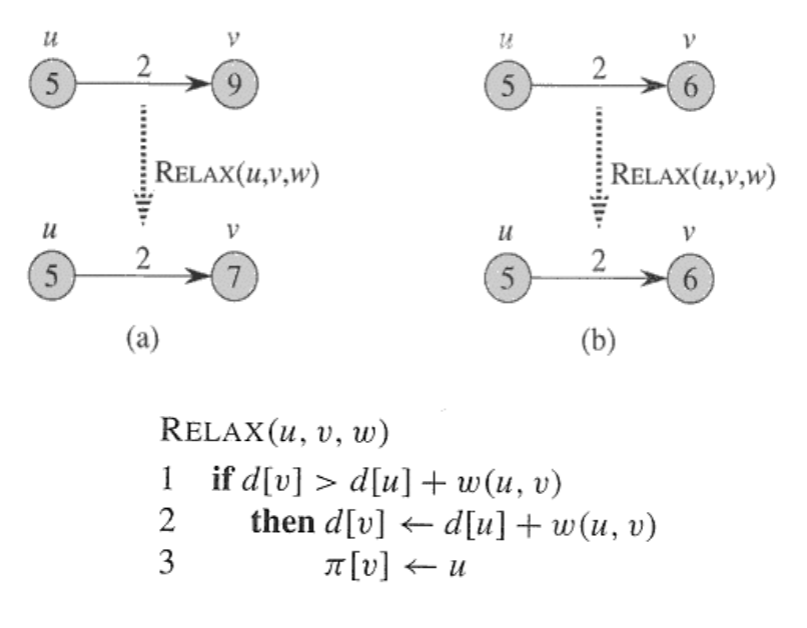
6. 기본연산 : Relaxation

  • 어떤 엣지에 대해서 relax한다.

  • 엣지 (u, v)에 대해서 relaxe한다. 무슨 의미이냐.
  • d[u] = 5, d[v] = 9는 각각 노드 S(출발지)에서 해당 노드까지 걸리는 최종 최소 거리 값이다.
  • 따라서 d[u] = 5는 노드 s에서 u까지 5의 거리는 의미이다.
  • 똑같이 d[v] = 9는 노드 s에서 v까지 9의 거리를 의미한다.
  • 이때 u에서 v까지 가는 거리가 2라고 한다고 하자.
  • 그러면 s에서 v까지 가는 거리가 9였는데 u를 지나처 v로 간다면 경로고 7이 된다.
  • 따라서 d[v]는 7이 된다.
  • 이를 relax한다라고 한다. (여기까지가 왼쪽 그림)
  • 오른쪽 그림의 경우 relax해도 경로가 더 커지므로 그냥 내비둔다.

7. 기본 알고리즘 (Bellman-Ford 알고리즘)

  • 대부분의 single-source 최단경로 알고리즘의 기본 구조
    1. 초기화: d[s]=0, 노드 v≠s에 대해서 d[v]=∞,π[v]=NIL.
    2. 에지들에 대한 반복적인 relaxation
  • 알고리즘들 간의 차이는 어떤 에지에 대해서, 어떤 순서로 relaxation 을 하느냐에 있음

  • 일반적인 single-source 알고리즘이다.
  • 여기서 변형시켜 나간다.
  • 1줄은 초기화. d[s]=0, 노드 v≠s에 대해서 d[v]=∞,π[v]=NIL
  • 3줄 부터. 각 엣지에 대해서 relax한다.
  • 5줄은 3줄에서 각 엣지에 대해서 relax에 했을 때 노드에 있는 relax한 값들이 변하지 않았다면 종료.
  • 아니면 다시 3번으로 가서 relax를 반복

7.1 최단 경로가 되는 이유

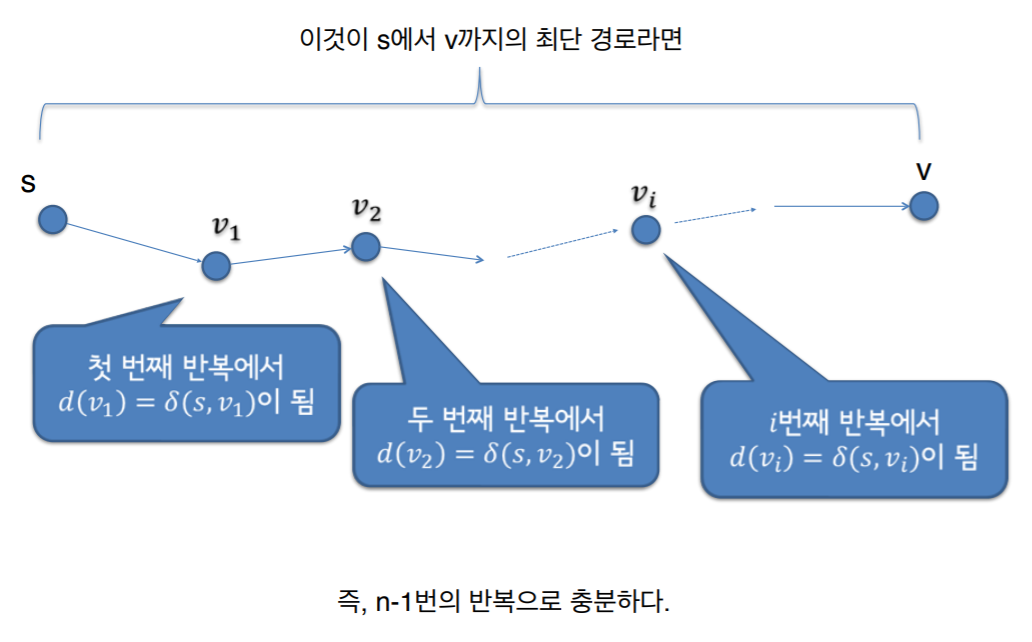
  • 어떤 그래프에서 s에서 v까지 최단 경로로 갈때 가장 많이 지날 경로의 수는 n-1개 이다. (N은 엣지의 갯수)

  • 첫 번째 반복일 때 d[s] = 0이고 d[v1]= w(s, v1) 이다. 이는 s에서 v까지의 최단 경로에서 s에서 v1로 가는 경로가 최단 부분 경로라는 것을 확인 할 수 있다.
  • 두 번째 반복일 때 relax가 되어 d[v2] = d[v1] + w(v1, v2)이다.
  • 이런 식으로 반복하면 n-1 반복으로 충분하며 최단 경로가 찾아진다.

7.2 Pseudo Code

  • 5번째 줄부터는 음수 사이클을 확인 하는 용도

  • 그래서 시간복잡도는 N-1 * M 즉, O(n*M)이다. M은 각 노드들이 가지고 있는 엣지의 개수

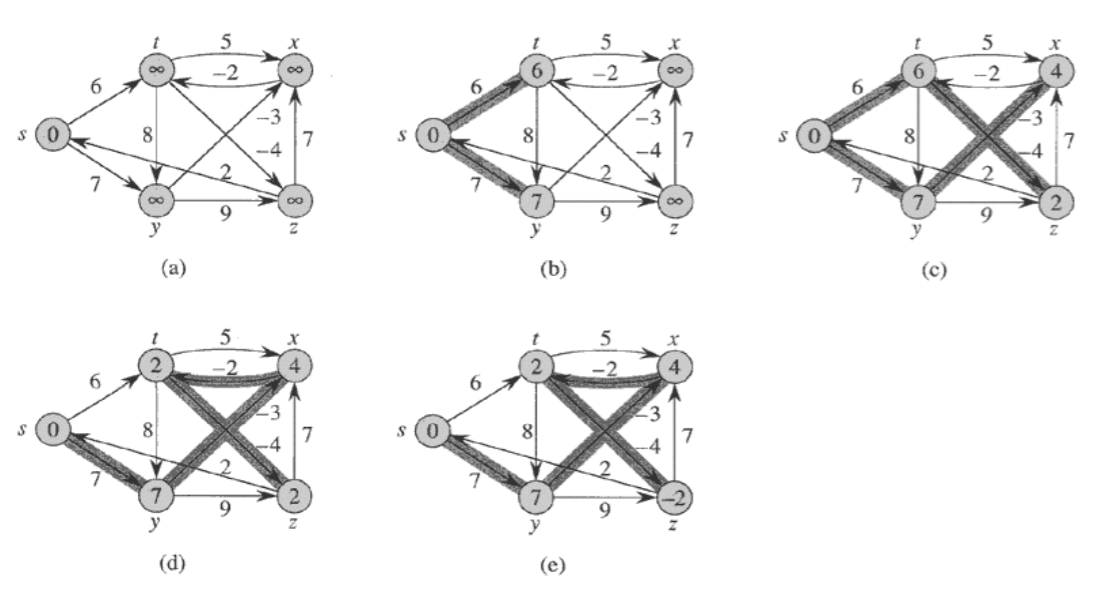
7.3 예시

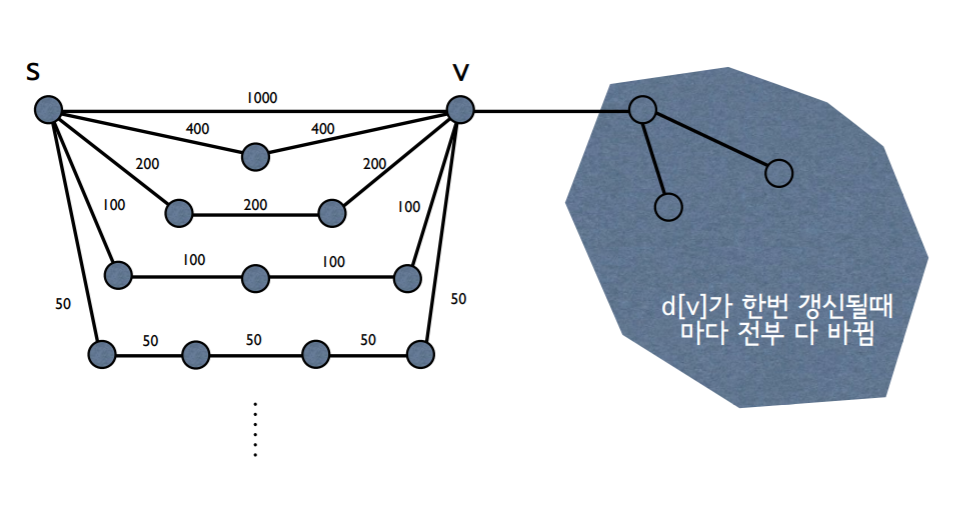
7.4 최악의 시나리오

  • S에서 V까지 가는 경로가 5가지라고 가정하자.
  • 처음 relax가 일어나면 V는 1000이 된다. 첫 번째 경로의 노드는 400, 그다음은 200.. 이렇게 된다.
  • 다음 relax가 일어나면 v는 800이 된다. 그러면 처음 relax가 되어 v가 1000이 되었을 때 v로부터 시작되는 엣지들은 1000인줄 알고 계산이 되었는데 800으로 바뀌니 또 다 계산 되어야 한다.
  • 하지만 3번째 relax가 일어나면 v는 500이 되고 또 v에서 시작하는 엣지들은 500으로 다 계산되어야 한다.

You may also enjoy