최소비용신장트리-03

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

Prim의 알고리즘

1. Prim의 알고리즘

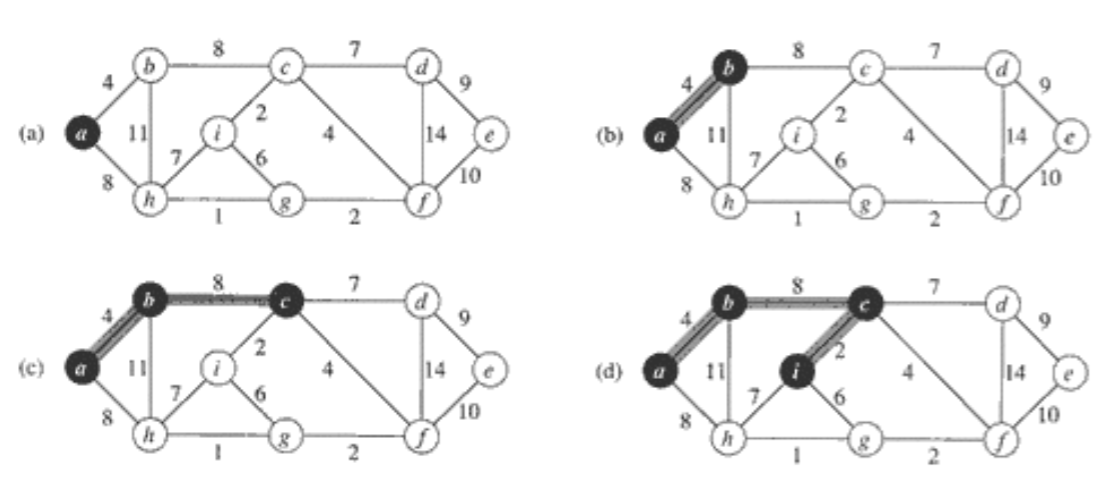
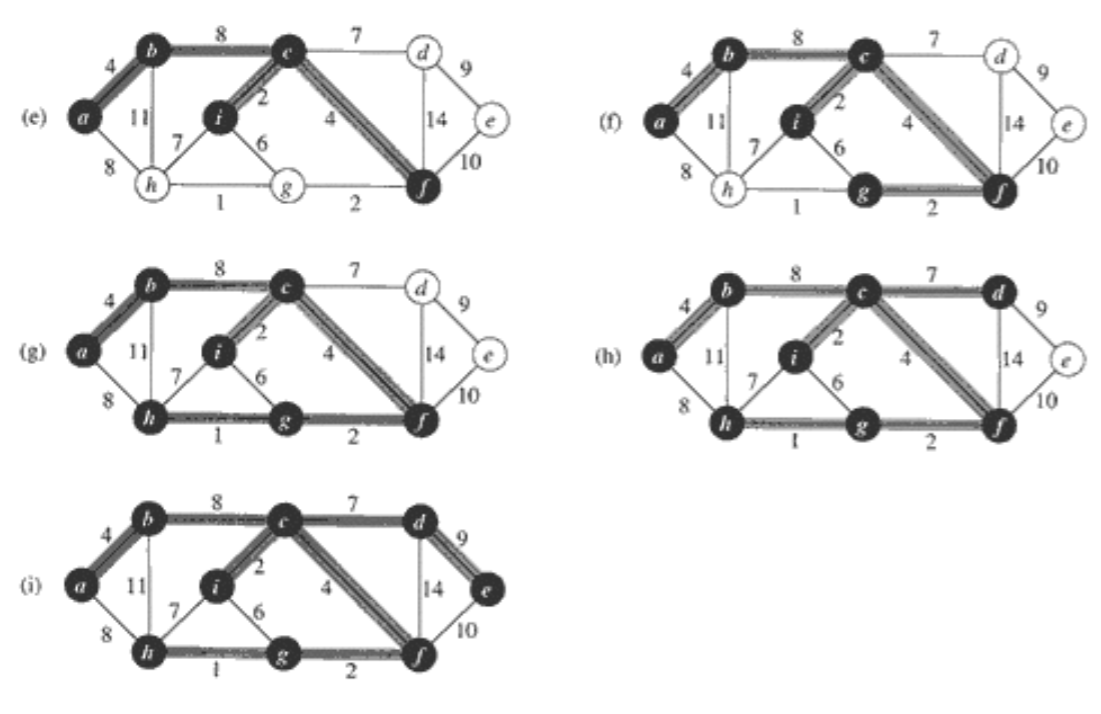
• 임의의 노드를 출발노드로 선택
• 출발 노드를 포함하는 트리를 점점 키워 감.
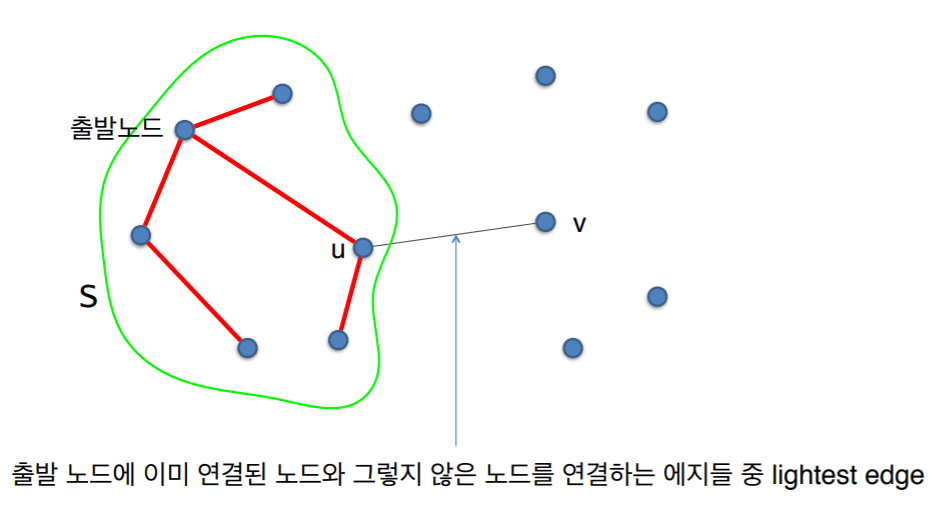
• 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 에지들 중 가장 가중치가 작은 에지를 선택

2. 왜 MST가 찾아지는가?

• Prim의 알고리즘의 임의의 한 단계를 생각해보자.
• A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

3. 가중치가 최소인 에지 찾기

• 위에 처럼 단순하게 알고리즘을 만든다면 최악의 경우 O(N^3)의 시간복잡도가 생김

• 이유는 예를 들어 집합 A에 있는 노드의 개수가 전체 노드에서 절반이 들어 있다면 N / 2개가 있다.

• 이때 A에 속하지 않는 노드들도 똑같이 N / 2개이다.

• 그렇다면 최악의 경우 A에 속한 노드들이 A에 속하지 않는 노드들에 모두 엣지가 있다면 에지의 개수는

  (N/2)^2. 즉, O(N^2)가 된다.

• 다시 말해서 하나의 최소 엣지를 찾기 위해서는 O(N^2)가 걸린다.

• 그러면 MST를 만들기 위해서는 N-1개의 엣지가 필요한데 각 엣지를 찾기 위해서 O(N^2)가 걸리므로 N*O(N^2). 즉, O(N^3) 시간 복잡도라는 계산이 나온다.

• 이는 MST를 만들기 위해서는 너무 비효율적이다.

3.1 향상된 prime

• V(A): 이미 트리에 포함된 노드들
• V(A)에 아직 속하지 않은 각 노드 v에 대해서 다음과 같은 값을 유지
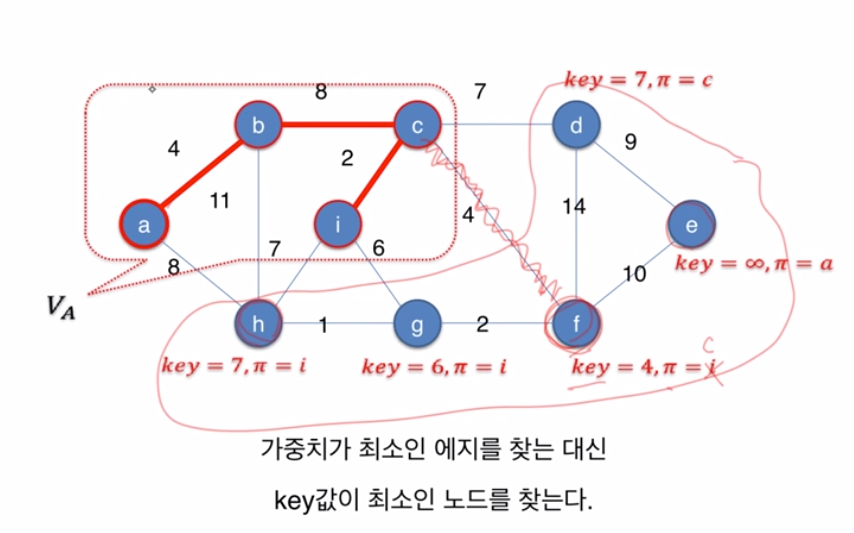
  • key(v): 이미 VA에 속한 노드와 자신을 연결하는 에지들 중 가중치가 최소인 에지 (u,v)의 가중치
  • π(v): 그 에지 (u,v)의 끝점 u

• 예를들어 노드 d의 경우 집합 V(A)에 연결된 끝 노드(즉, π(v))는 C이고 최소 가중치(즉, key(v))는 7이다.

• key가 무한대인 것은 연결 점이 없다는 의미

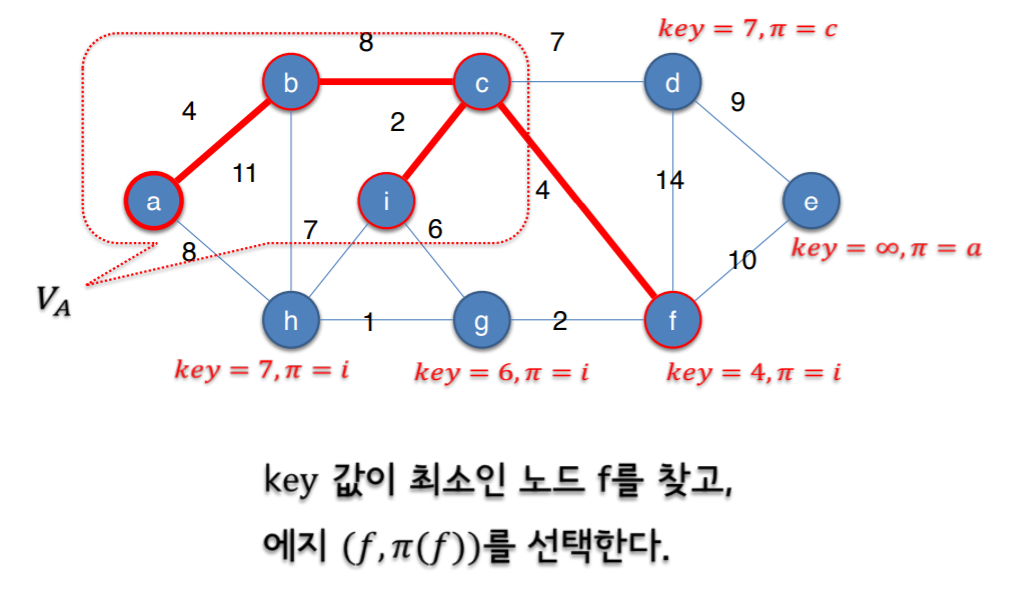
• 이렇게 되면 최소인 엣지를 찾는데 O(N) 정도 걸린다.
• 이때 설명이 안된 것은 key값을 찾는 걸린 시간. 위의 그림에서 f가 연결되면 나머지 연결되지 않는 노드들에 대해서 key값을 갱신하면 된다.
• 이때 걸리는 시간도 O(N) 걸린다.
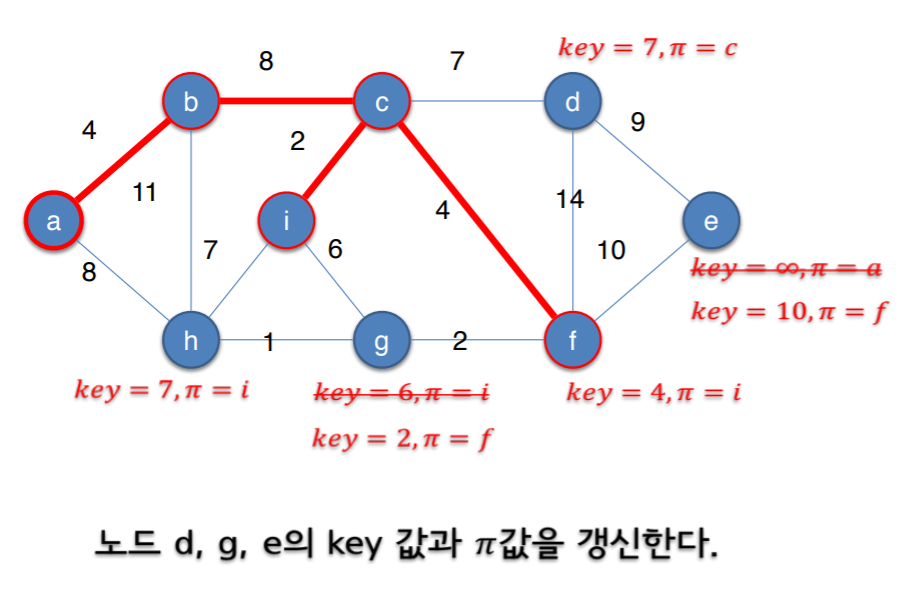
• 다시 돌아와서 f가 연결되었다면 노드 d를 보자. 이전 노드의 key값은 7이었는데 d는 f와의 엣지도 있다. 이때 기존의 key값과 d와 f의 엣지 가중치를 비교하여 둘 중 더 최소 가중치를 key값으로 셋팅한다.
• 따라서 d와 f의 가중치는 14이므로 기존의 key값의 7보다 가중치가 크므로 그대로 둔다.
• g의 경우 key값이 6이고 파이가 i였으나 f가 연결되고 나서 (g, f) 엣지와 비교하니 가중치가 더 좋으므로 key가 2로 파이가 f로 바뀐다.

3.2 시간복잡도

• r은 출발점
• 인접행렬로 하나 인접리스트로 하나 똑같이 O(N^2) 시간복잡도 걸림

4. key 값이 최소인 노드 찾기

• 최소 우선순위 큐를 사용
• V-V(A)에 속한 노드들을 저장
• Extract-Min : key 값이 최소인 노드를 삭제하고 반환

4.1 MST 최소 우선순위 큐 Pseudo Code

• 이진 힙(binary heap)을 사용하여 우선순위 큐를 구현한 경우
• while loop:
  • n번의 Extract-Min 연산: O(nlogn) . 순수 extract-min은 logN인데 n번 extract해야하니까
  • m번의 Decrease-Key 연산: O(mlogn) 이것도 위와 같음 재 정렬하는데 M(N*N)번 걸림
• 따라서 시간복잡도: O(nlogn + mlogn) = O(mlogn)
• 우선순위 큐를 사용하지 않고 단순하게 구현할 경우: O(n2)
• Fibonacci 힙을 사용하여 O(m+nlogn)에 구현 가능[Fredman-Tarjan 1984]