최소비용신장트리-02

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

Kruskal의 알고리즘

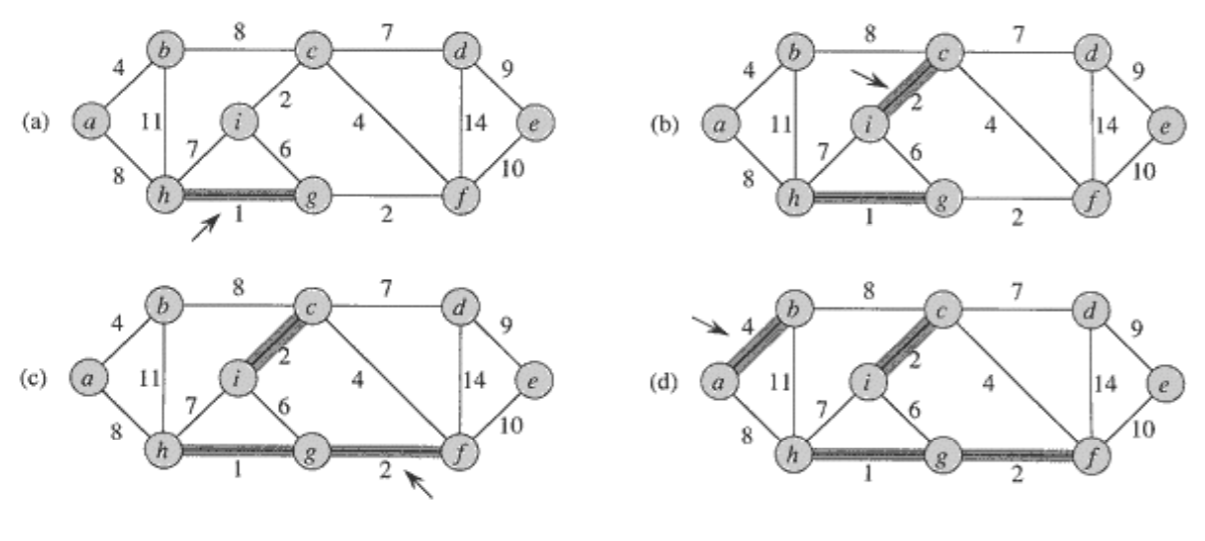
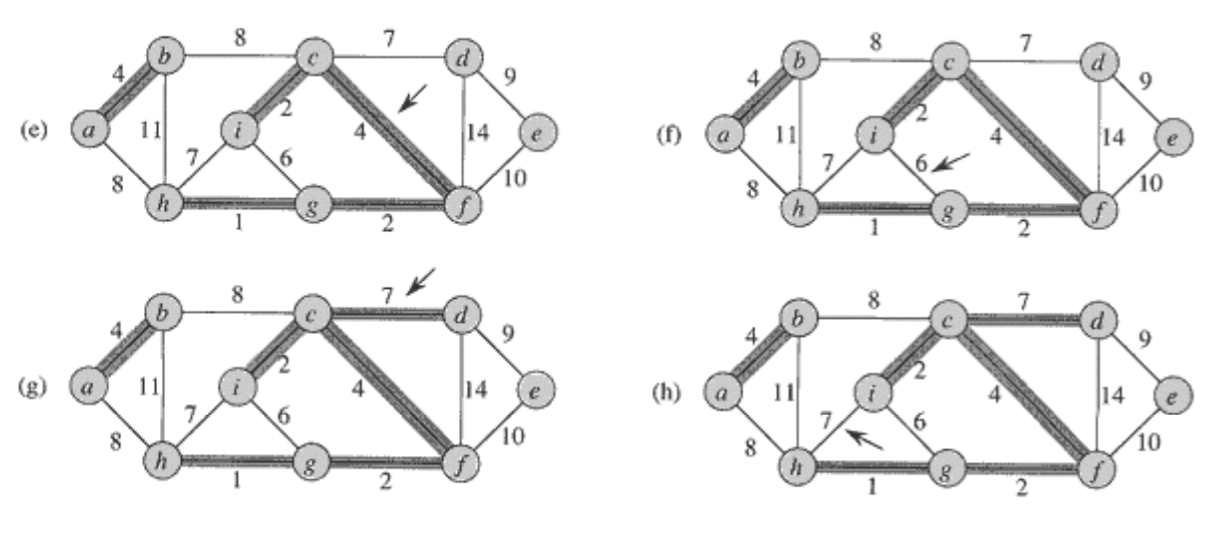
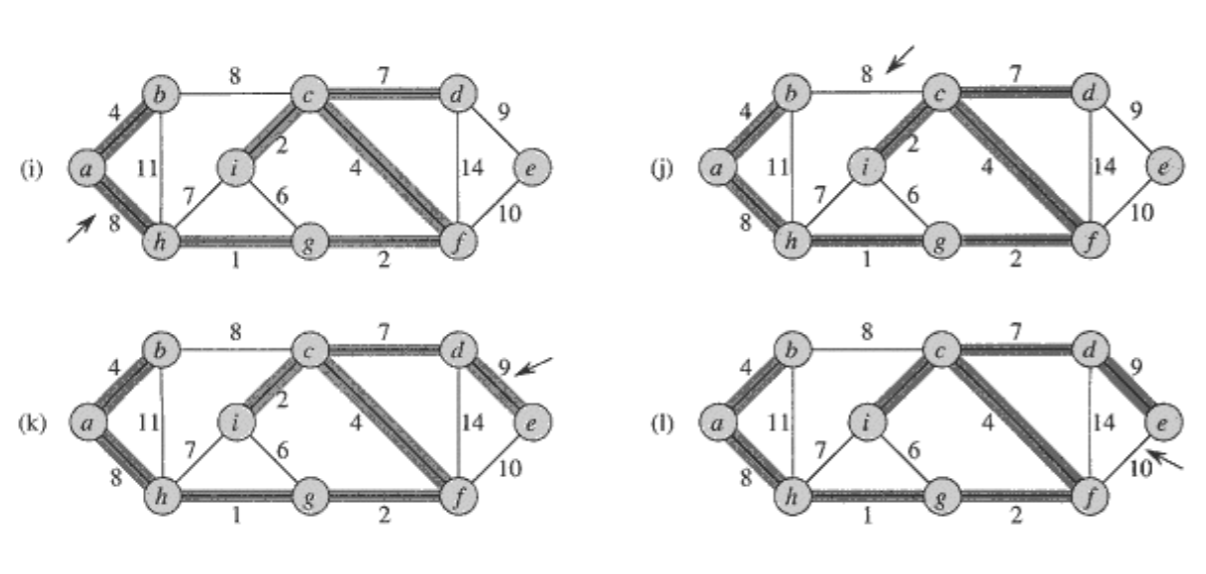
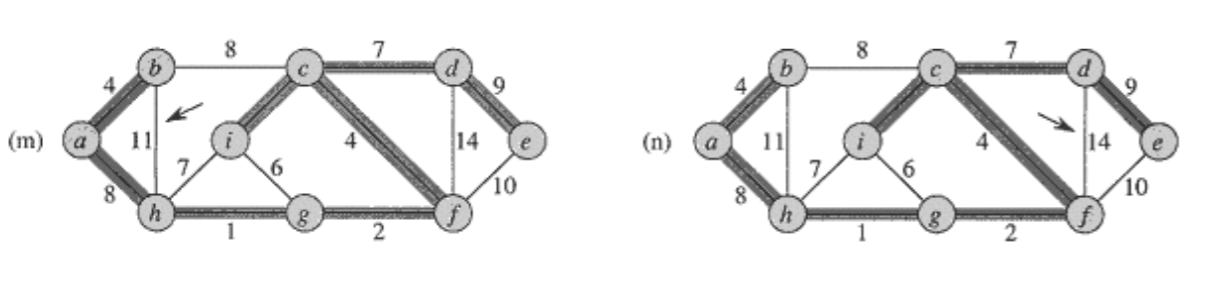
1. Kruskal의 알고리즘

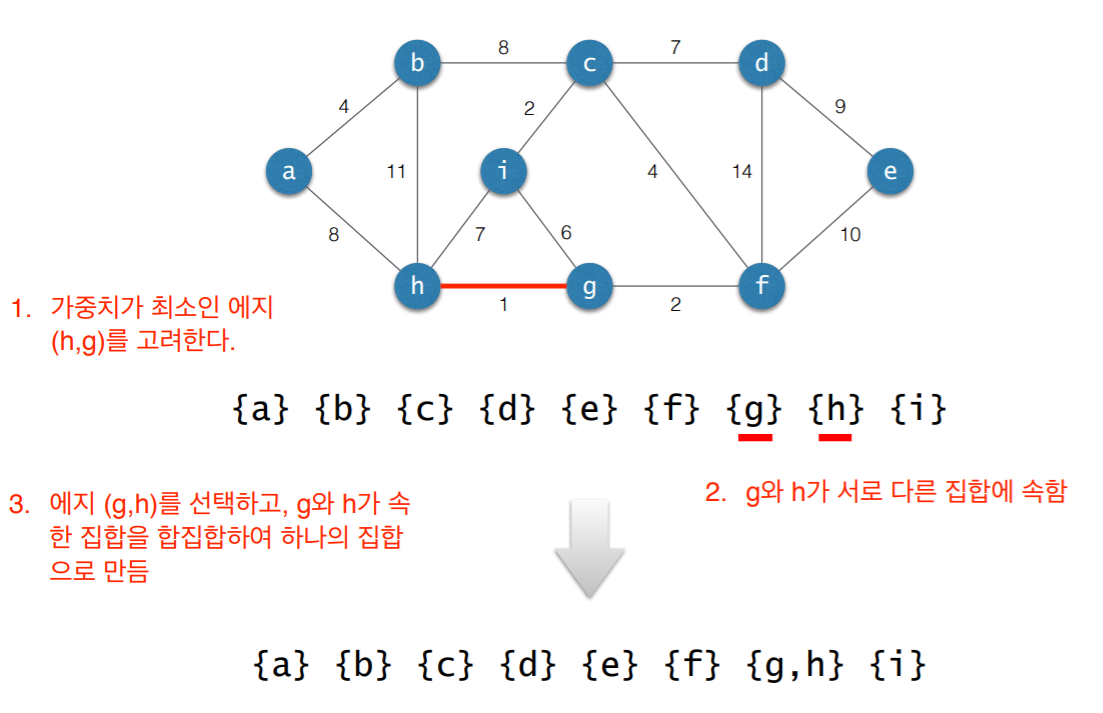
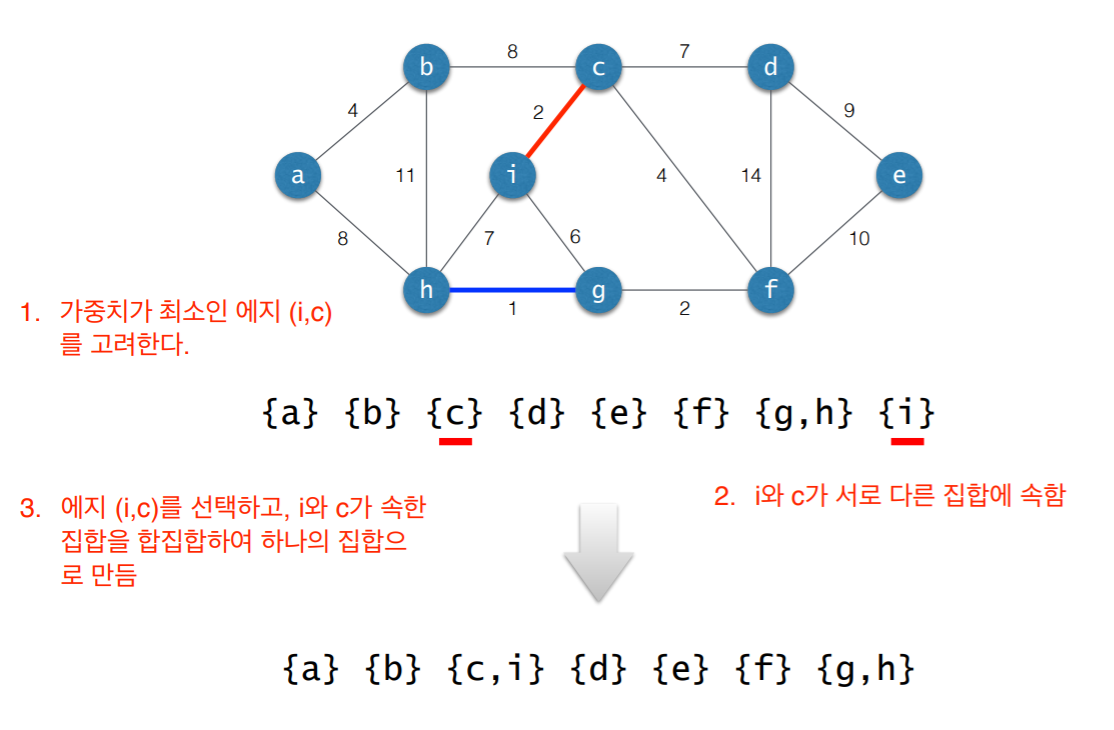
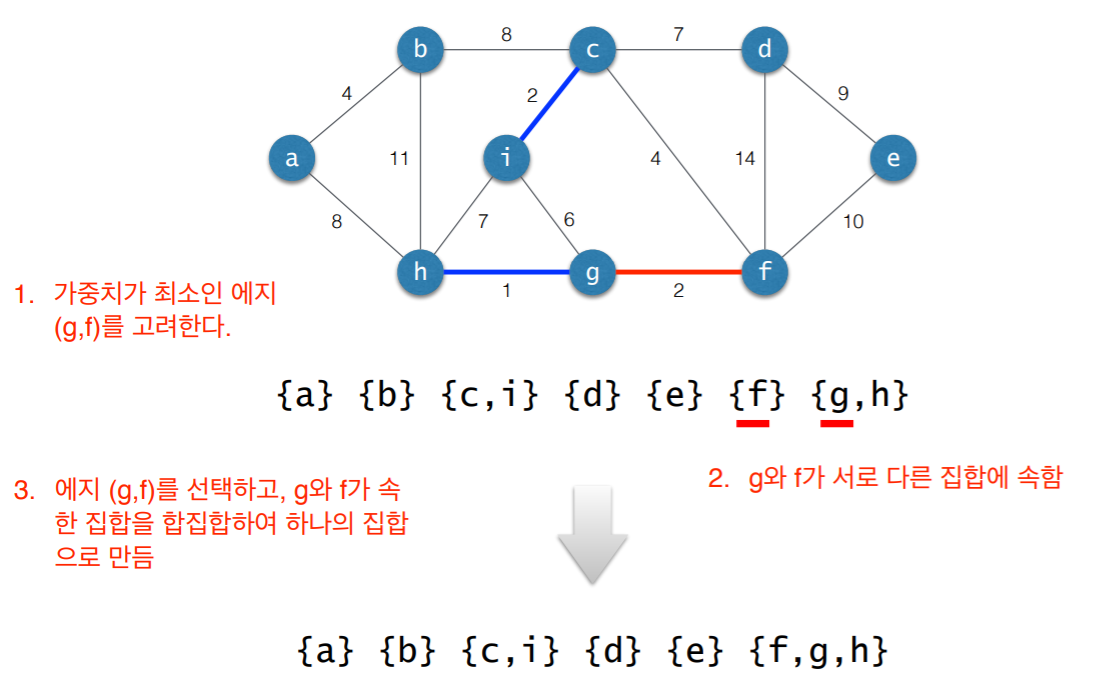
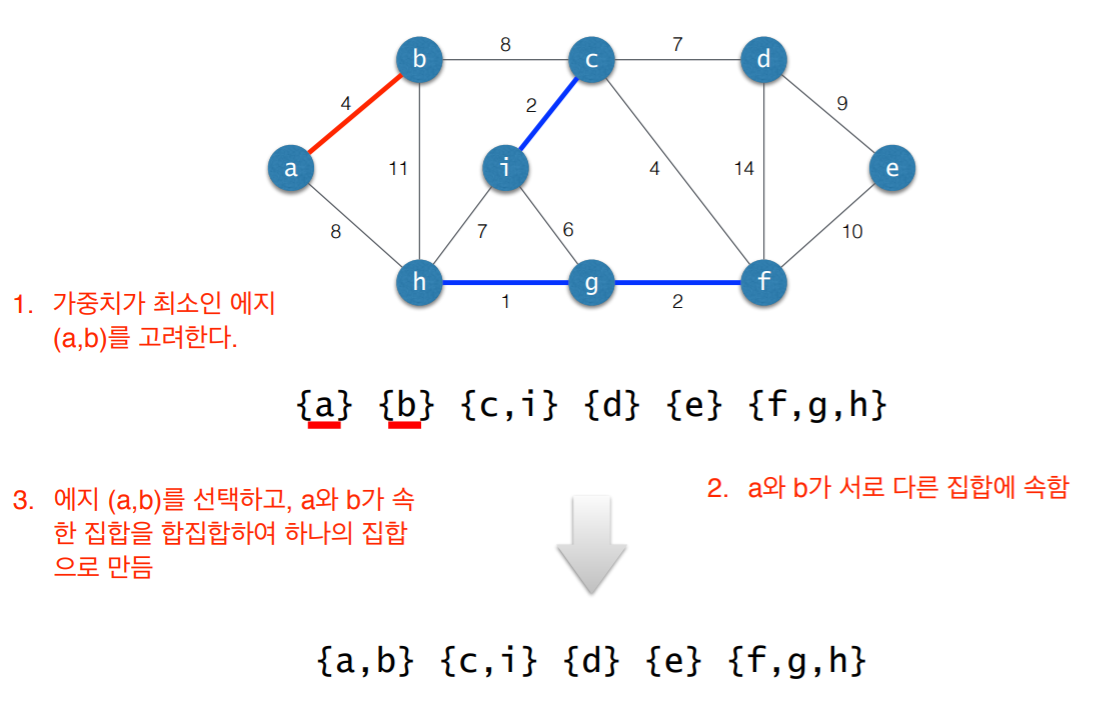
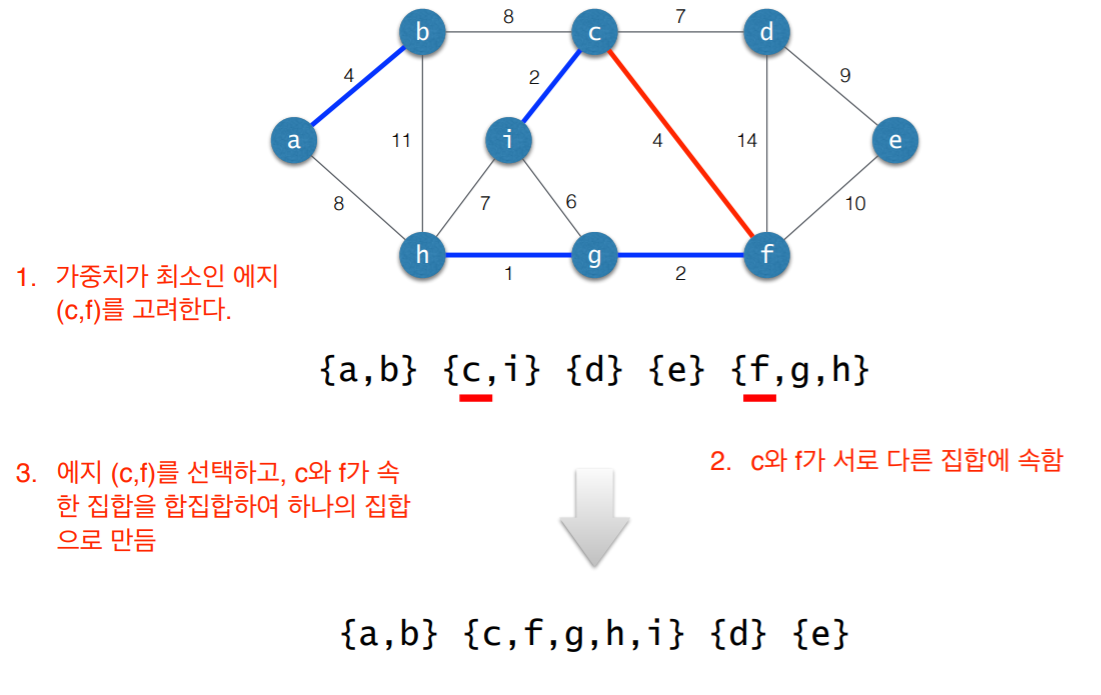
• 에지들을 가중치의 오름차순으로 정렬한다.
• 에지들을 그 순서대로 하나씩 선택해간다.
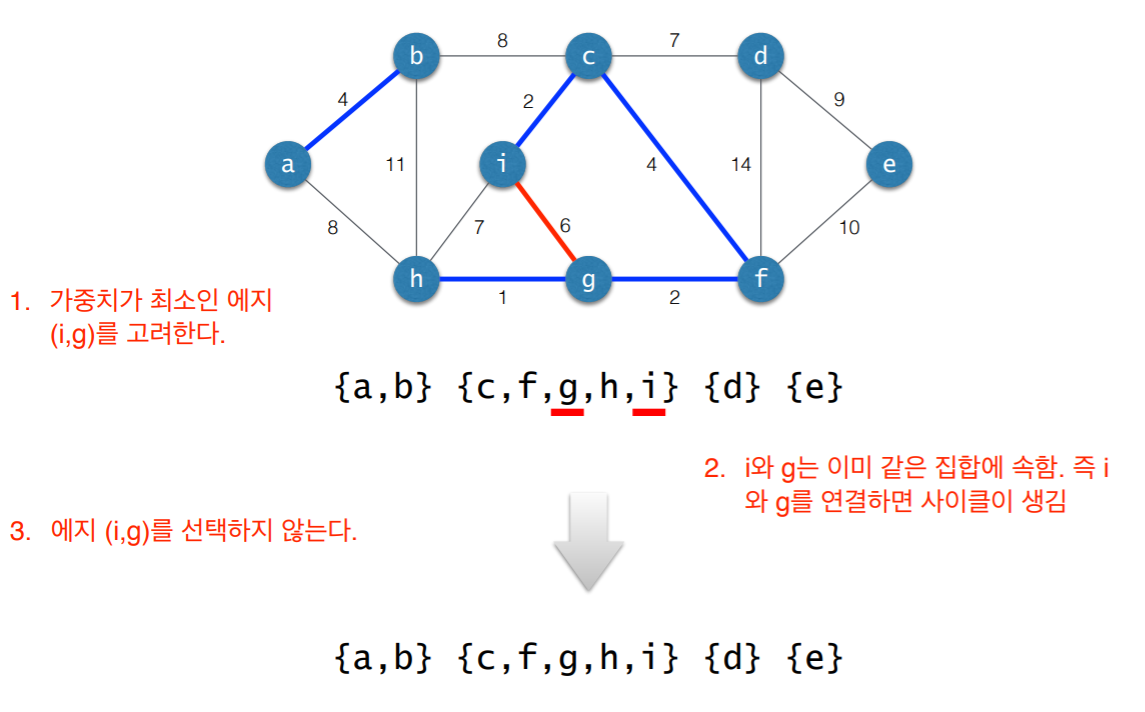
• 단, 이미 선택된 에지들과 사이 클(cycle)을 형성하면 선택하지 않는다.
• n-1개의 에지가 선택되면 종료한다.

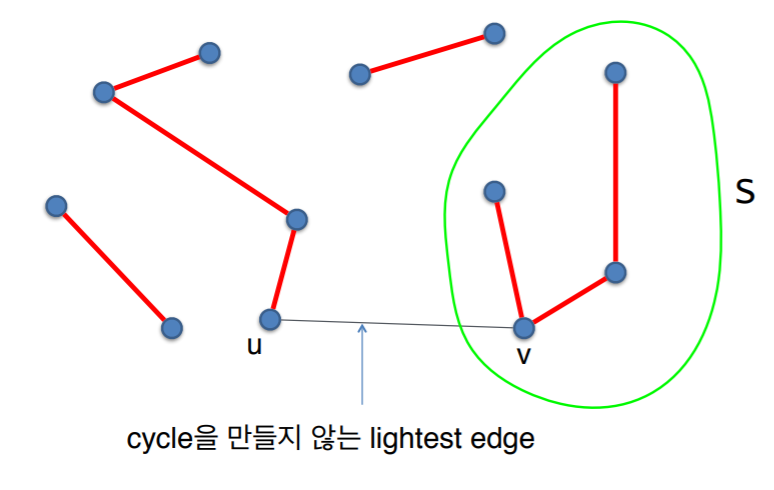
2. 왜 MST가 찾아지는가?

• Kruskal의 알고리즘의 임의의 한 단계를 생각해보자.
• A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

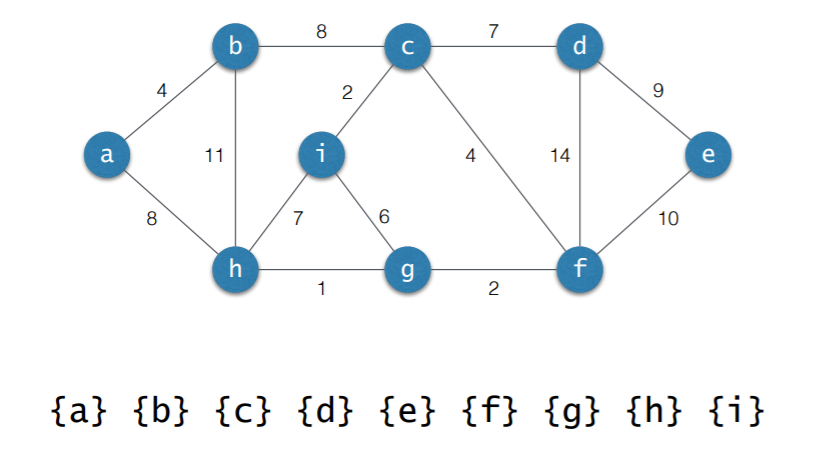
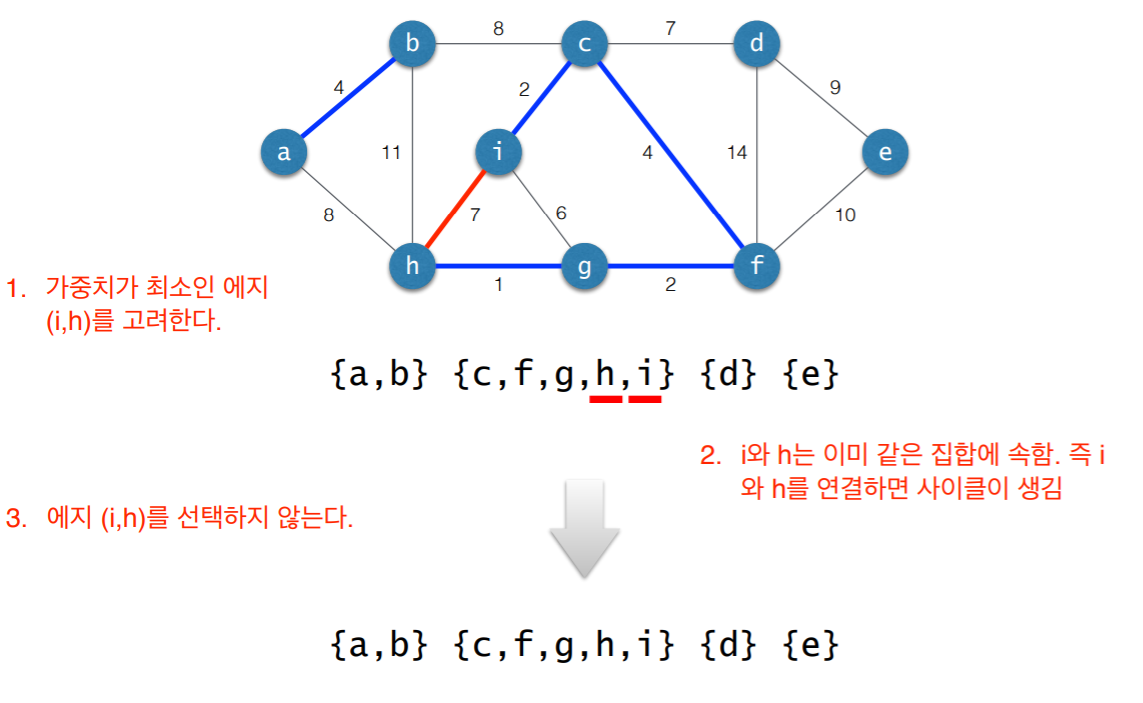
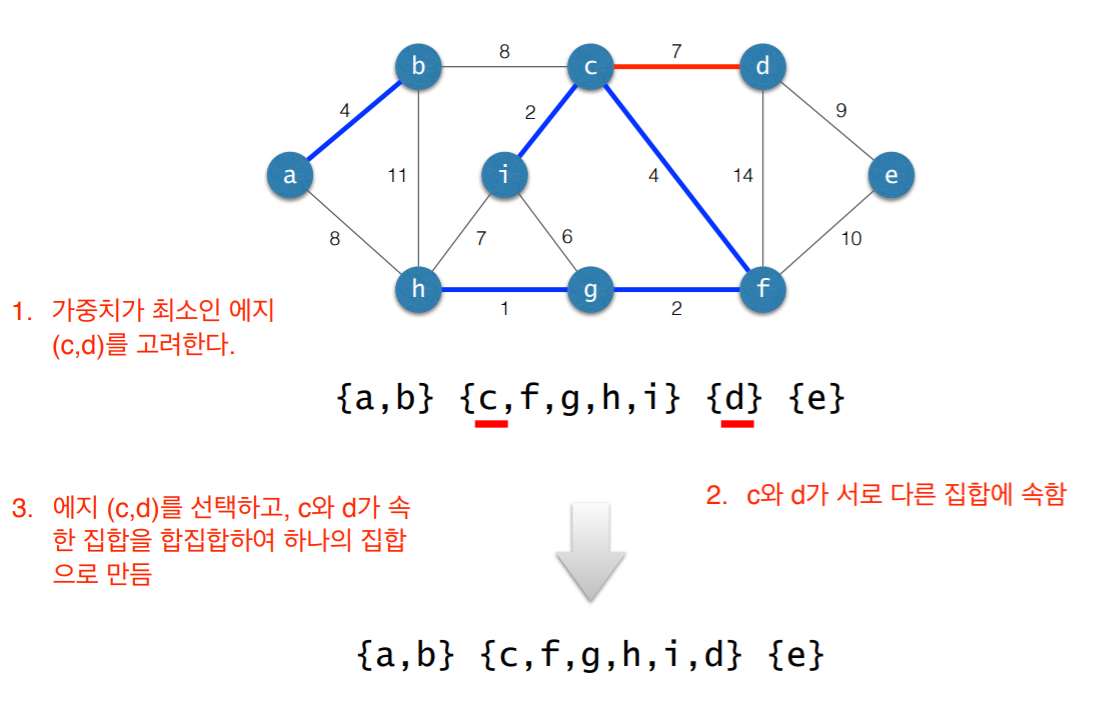
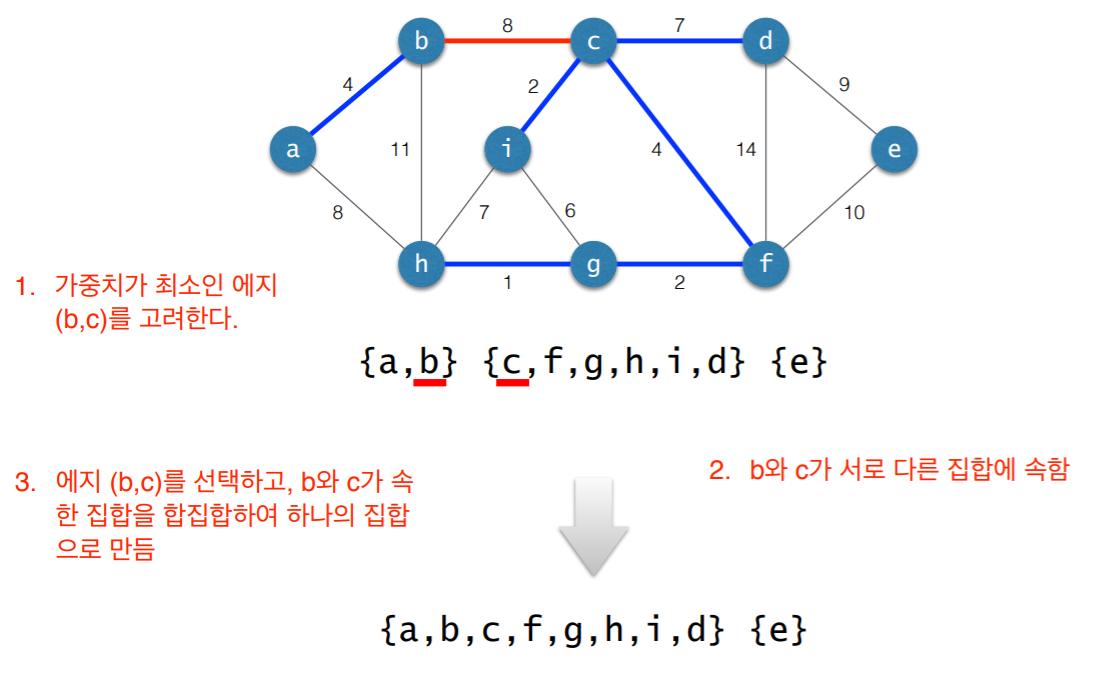
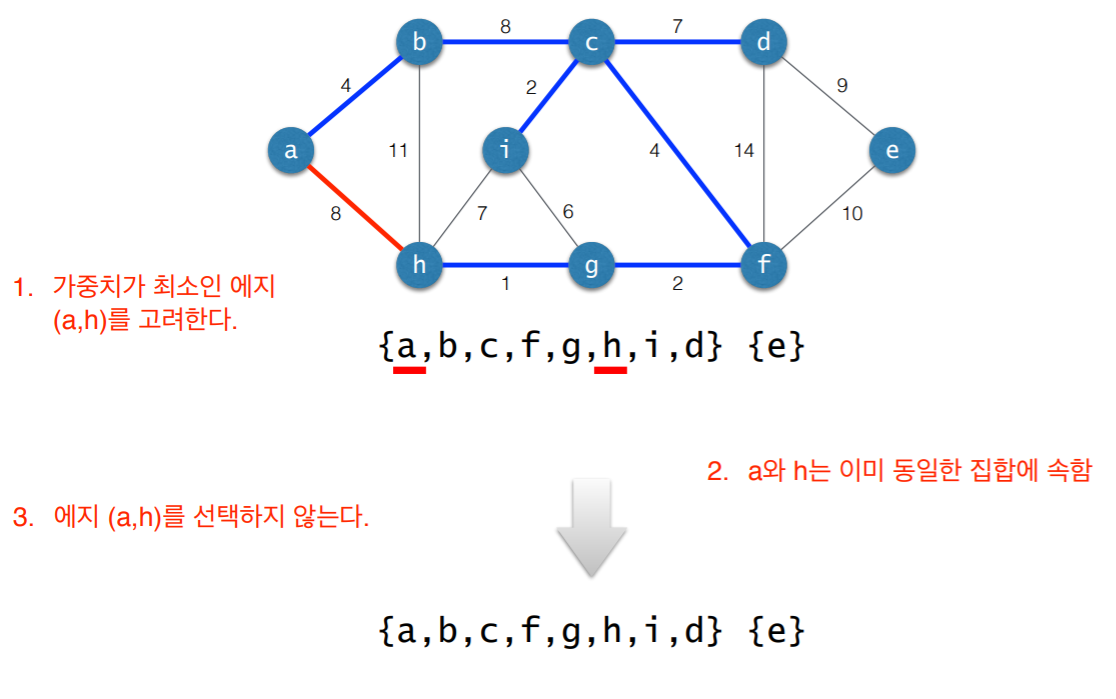
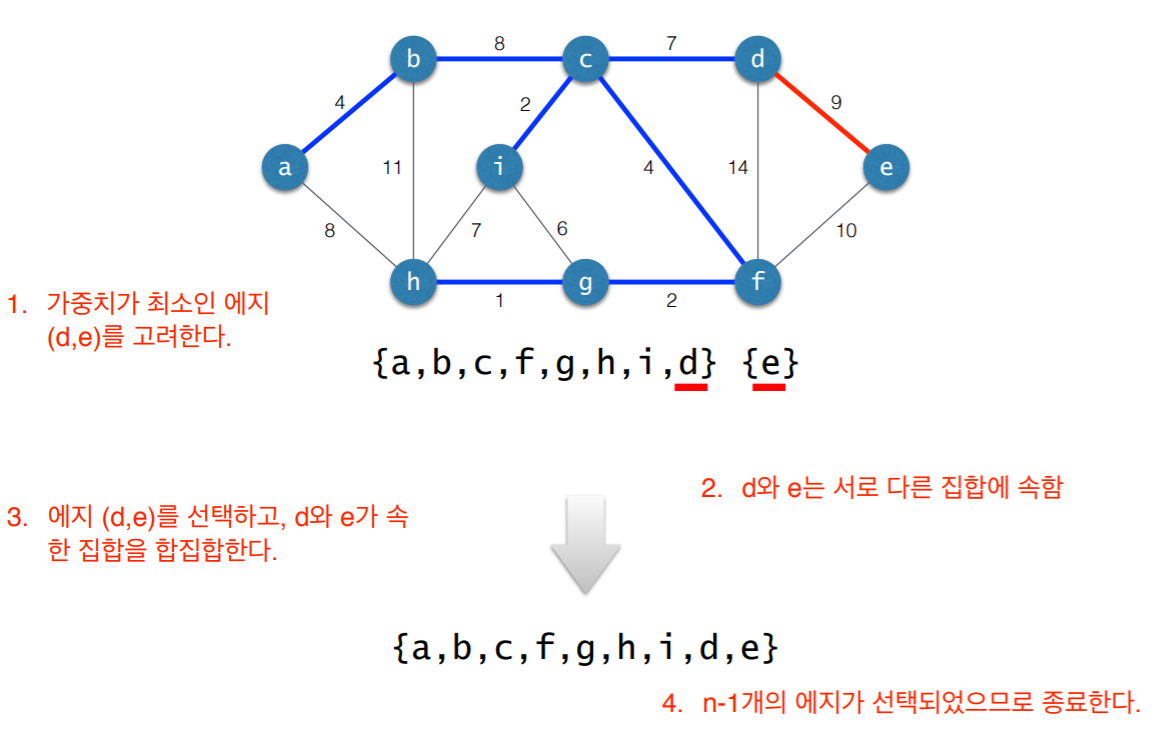
3. 사이클 검사

• 초기 상태: 선택된 에지 없음
• 각각의 연결요소를 하나의 집합으로 표현

4. Pseudo Code

4.1 서로소인 집합들의 표현

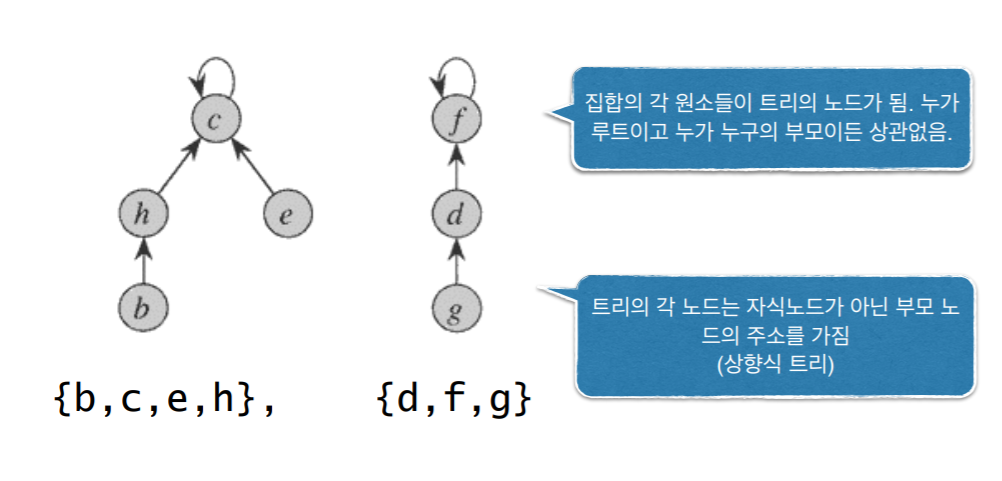
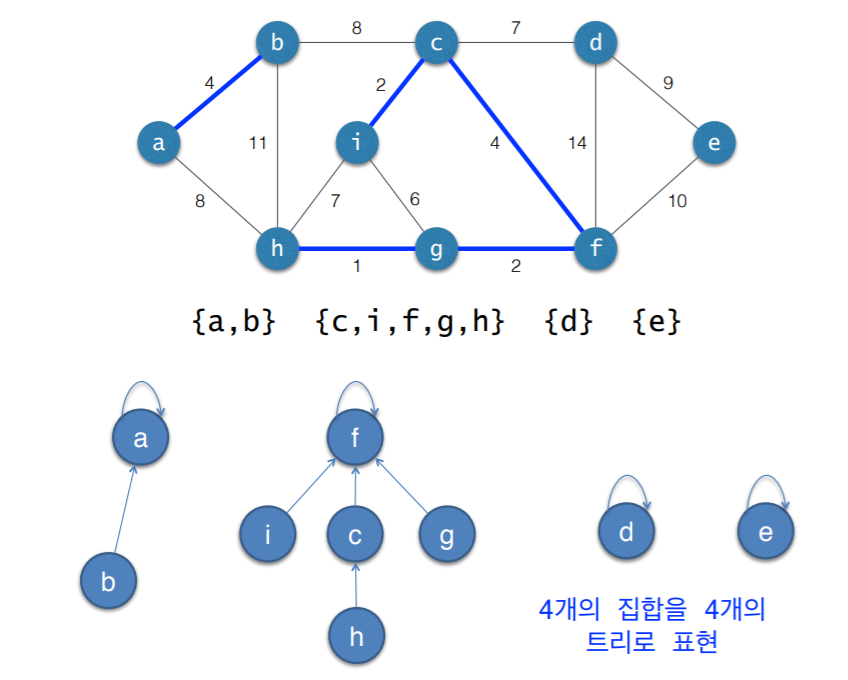
• 각 집합을 하나의 트리로 표현

• 보통의 트리는 자식 노드의 주소를 가지는 하향식 트리임. 그러나 여기선 상향식 트리

• 누가 부모여도 상관 없음. 집합 {a, b}에서 a든 b든 아무나 부모 노드가 되어서 트리 형태이면 됨

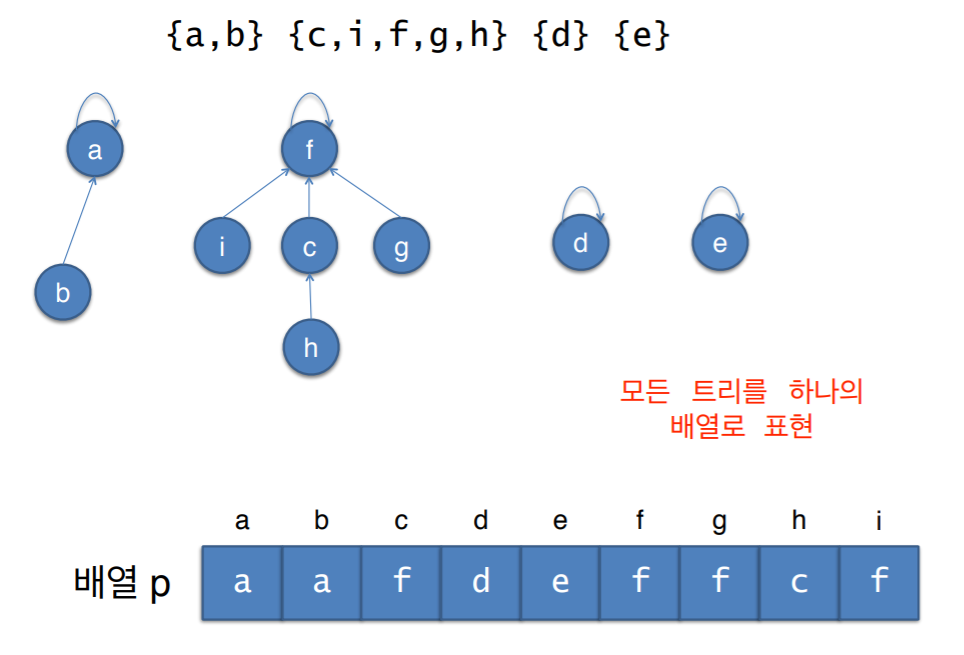
• 각 노드의 부모 노드를 각 노드의 순서대로 배열로 표현
• 모든 트리를 하나의 배열로 표현 가능하다.

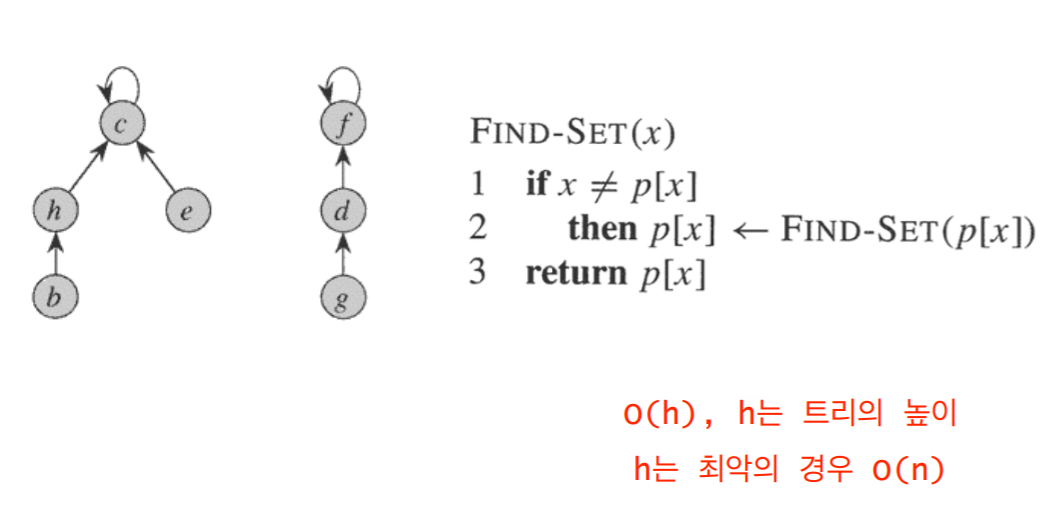
4.2 Find-Set(v)

• 자신이 속한 트리의 루트를 찾음

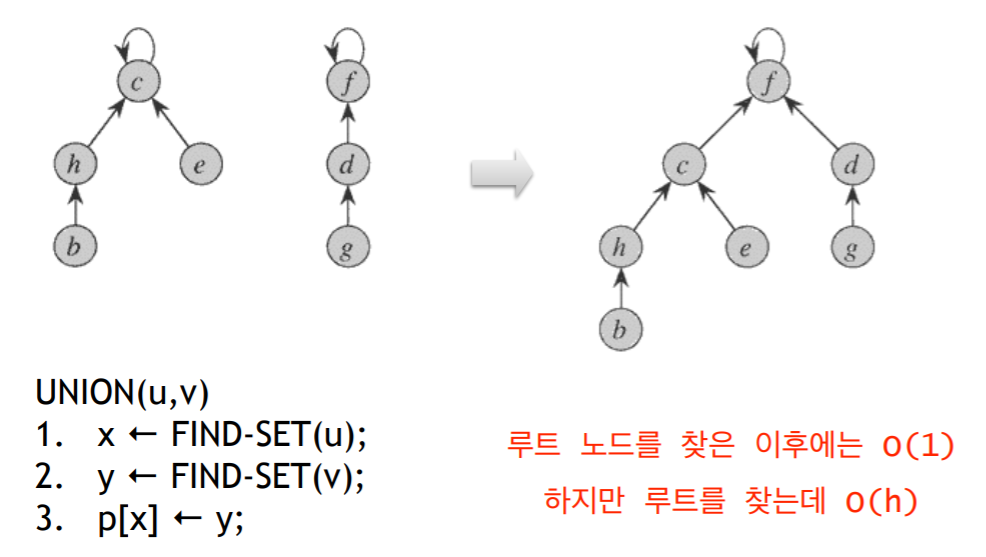
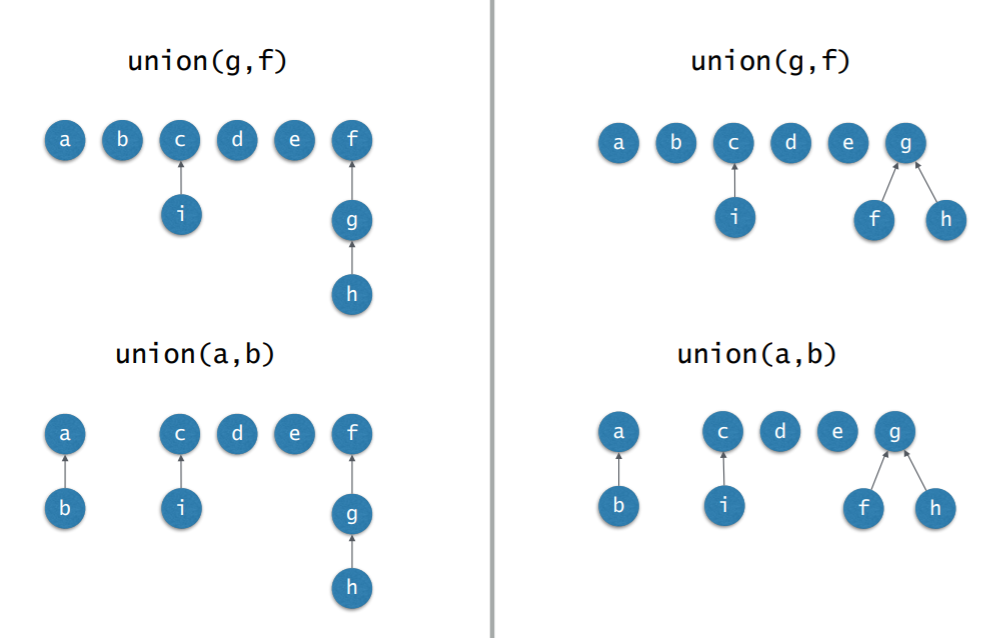
4.3 Union(u, v)

• 한 트리의 루트를 다른 트리의 루트의 자식 노드로 만듬

• 위에서는 C가 F의 자식 노드로 가는데 반대로 해도 상관 없음.

5. Weighted Union

• 지금 까지의 시간 복잡도는 O(m * n)이다.
• m은 노드의 개수. n은 각 노드들이 find-set하는 걸리는 시간

• 위에 알고리즘을 조금 바꾸면 시간복잡도를 향상시킬 수 있다. 그게 weighted Union

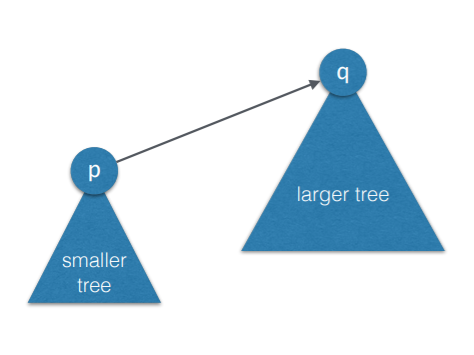
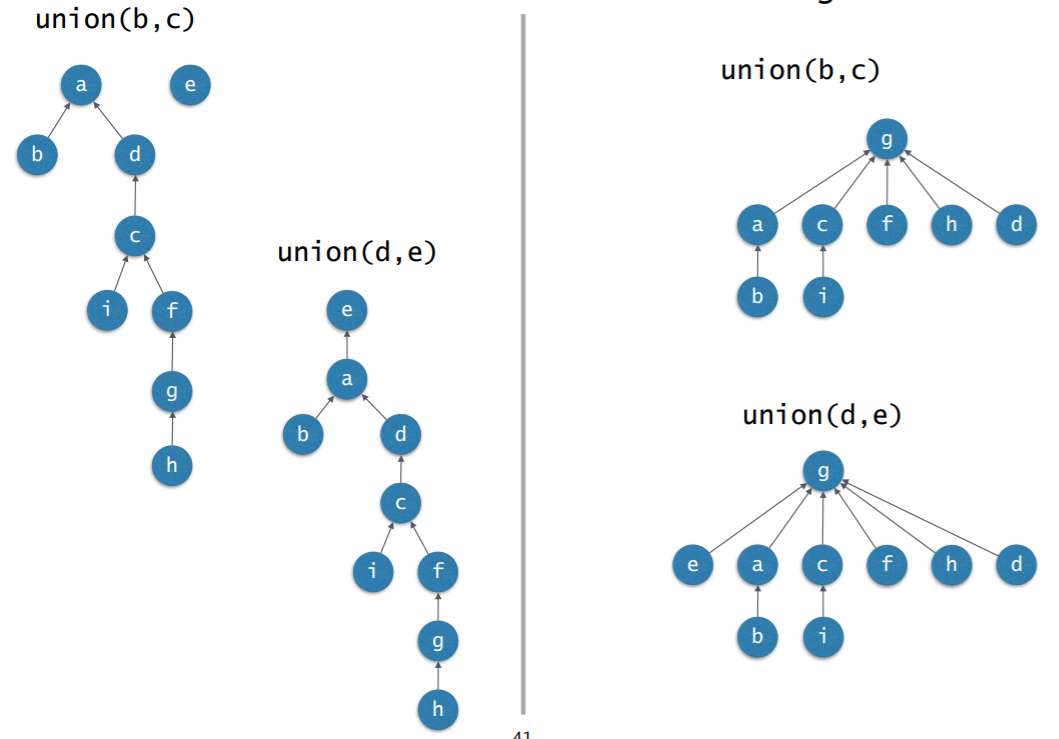
• 두 집합을 union할 때 작은 트리의 루트를 큰 트리의 루트의 자식으로 만듬 (여기서 크기란 노드의 개수)
• 각 트리의 크기(노드의 개수)를 카운트하고 있어야 한다.
• 즉, 노드 개수가 적은 트리가 노드 개수가 많은 트리의 자식이 되야 한다는 이야기

WEIGHTED-UNION(u,v){
	x <- FIND-SET(u);
	y <- FIND-SET(v);
	
	if(size[x] > size[y]) then
		p[y] = x;
		size[x] <- size[x] + size[y];
	else
		p[x] = y;
		size[y] <- size[y] + size[x];
}

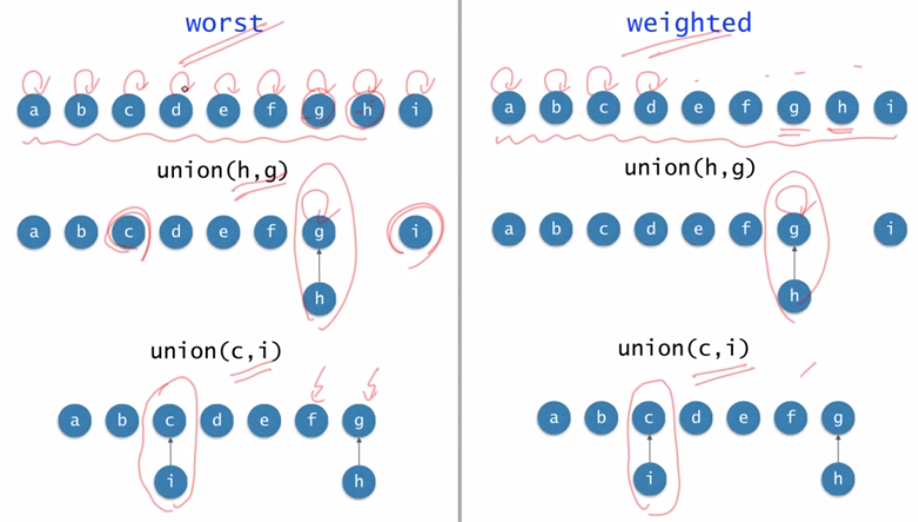
5.1 Worst vs Weighted Union

• Union할 때 사용

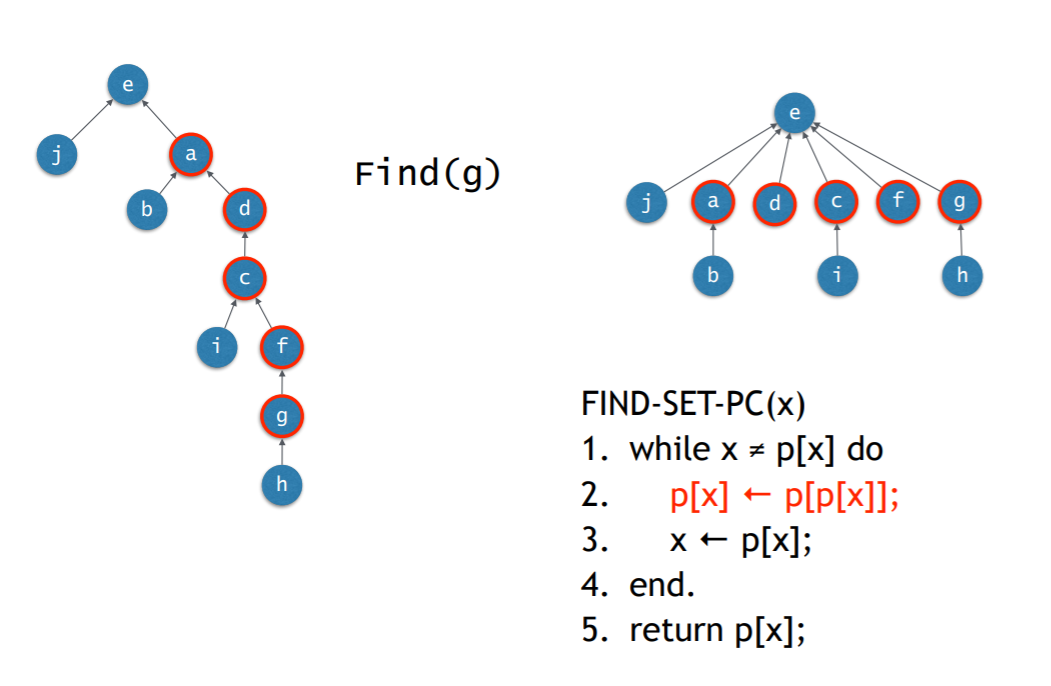
5.2 Path Compression(압축)

• Find할 때 사용
• Find하면서 지나가는 노드들을 모두 최상의 부모노드의 자식으로 만든다.
• 실제 그렇게 하는게 아니라 일단 최상의 부모 노드를 찾아놓고 원래 노드로 돌아와서 찾아놓은 부모노드에 연결한다.
• 아래 코드는 위에 말한 내용은 아님. 단순히 왼쪽그림에서 반정도 줄여주는 느낌.
• 위에서 말한 내용을 구현하려면 2번줄을 삭제하고 밑에 다시 while문 하나를 더 넣어야 함. 그렇게 하면 오른쪽 그림처럼 됨.
• 시간 복잡도 측면에서는 while 문 2개 쓰는게 나음

5.3 Weighted Union with Path Compression

• M번의 union-find 연산의 총 시간복잡도는 O(N+Mlog*N).
• 여기서 N은 원소의 개수
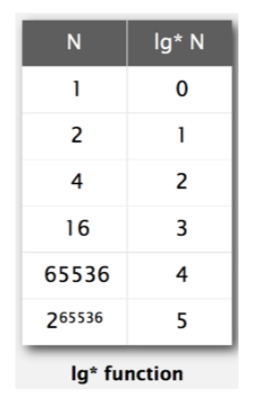
• log*N은 (여기서 log는 log2N을 말함) 몇 번 log를 해야 1이 되는지 말함.
• 아래 표를 보면 N이 2일 때 log를 하면 1이다. 따라서 log*N은 1이다. (log를 한 번 사용 했기 때문)
• N이 16일 때는 log를 3번 사용한다. log16은 4이고 다시 log하면 2이고 다시 2에 log하면 1이다.
• 따라서 log를 3번 사용했기 때문.

• 거의 선형시간 알고리즘, 즉 한 번의 Find혹은 Union이 거의 O(1)시간

6. 시간복잡도

• 각 노드들의 부모노드를 자신으로 만드는데 걸리는 loop
• 모든 에지들을 가중치 순으로 정렬 시간 (MlogM)
• 두 번의 Find-Set은 O(1)이고 Union은 O(m)이므로 두 번째 loop는 대략 O(m)이다.
• 즉, 크루스칼 알고리즘에서 시간복잡도에 영향을 미치는 것은 엣지들을 정렬하는 부분

• 그래서 O(

  E

  log2

  E

  )이라고 하는데 바꿔서 O(mlogm)이라고 함

• m는 n*(n-1) /2이다.
• 그래서 O(m log m)을 O(m log n^2)라고 할 수 있기 때문에 최종적으로 O( m log n)이다.