그래프에서의 DAG

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

DAG(Directed Acyclic Graph)

• DFS, BFS라고 해서 꼭 무방향 그래프에서만 적용되는 것은 아님
• 단지 원하는 노드에 도착하지 못할 수도 있다는 것 뿐

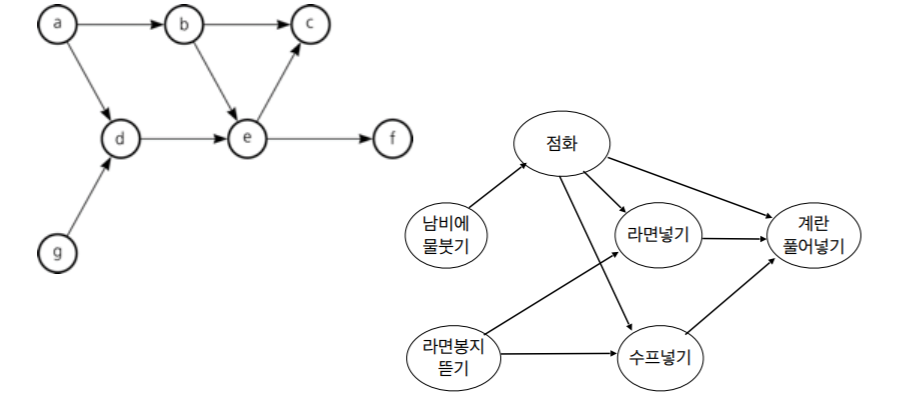
1. DAG(Directed Acyclic Graph)

• DAG는 방향 사이클(directed cycle)이 없는 방향 그래프.
• 예 : 작업들의 우선순위

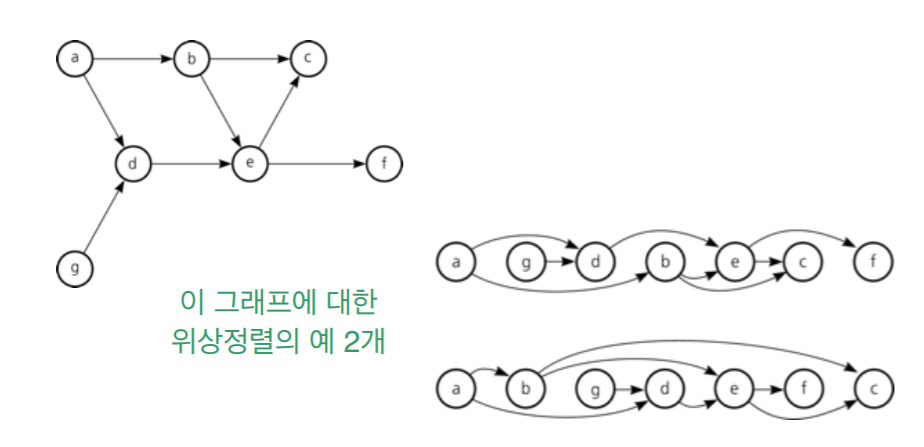
2. 위상정렬 (topological ordering)

• DAG에서 노드들의 순서화 v1, v2,…,vn, 단, 모든 에지 (vi,vj)에 대해서 i < j가 되도록.
• 왼쪽에서 오른쪽으로 가야한다.
• 역방향은 위상 정렬이 아니다.

• degree (들어오거나 다가는 경로)
• indegree(들어오는 경로), outdegree(나가는 경로)
• 맨처음 indegree가 없는 노드를 출력. a를 출력
• a의 outdegree를 삭제
• 그 다음 indegree가 없는 노드를 출력. g를 출력
• g의 outdegree를 삭제
• 그 다음 indegree가 없는 노드를 출력. b를 출력
• b의 outdegree를 삭제…
• 반복.

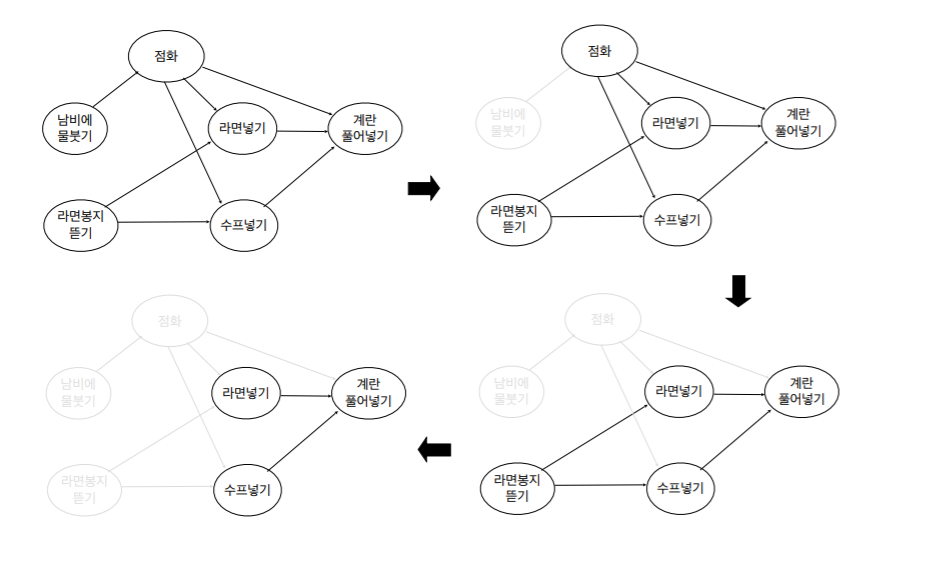
2.1 알고리즘 1

topologicalSort1(G)
{
    for ← 1 to n {
       진입간선이 없는 임의의 정점 u를 선택한다;      
       A[i] ← u;
       정점 u와 u의 진출간선을 모두 제거한다;  
    }
    ▷ 배열 A[1…n]에는 정점들을 위상정렬되어 있다
}

• 수행시간 O(n+m)

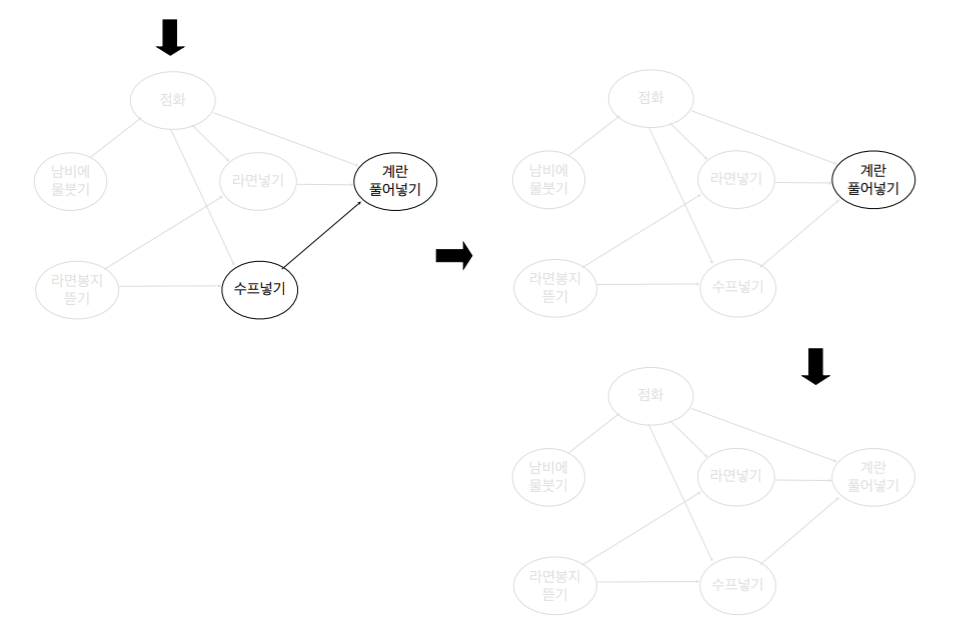
2.2 알고리즘 2

topologicalSort2(G)
{
    for each v∈V
       visited[v] ← NO;
 	make an empty linked list R;
    
    for each v∈V ▷ 정점의 순서는 상관없음
       if (visited[v] = NO) then
 			DFS-TS(v, R);  
} 

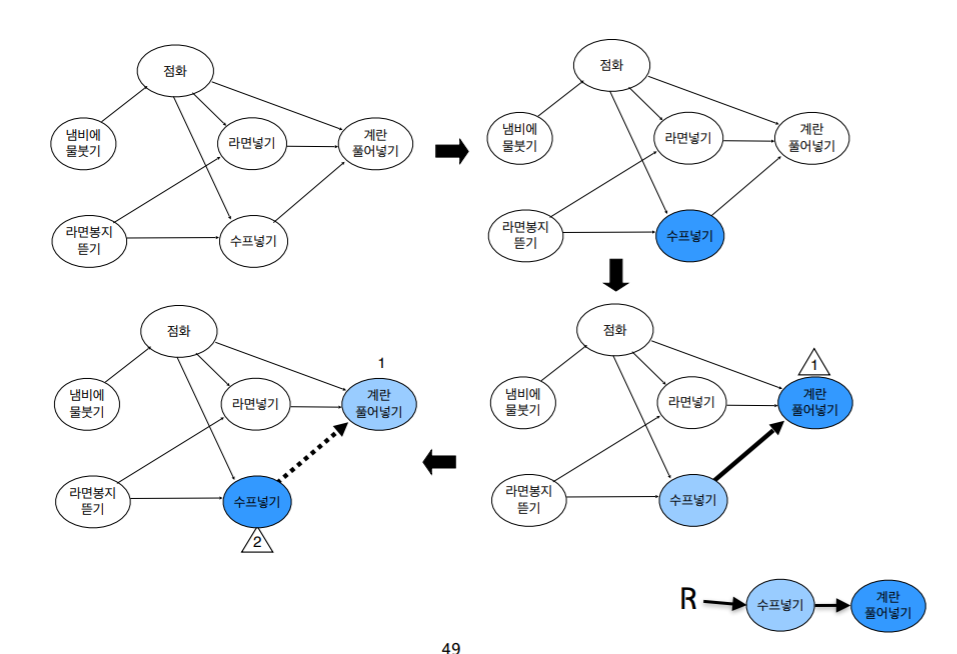
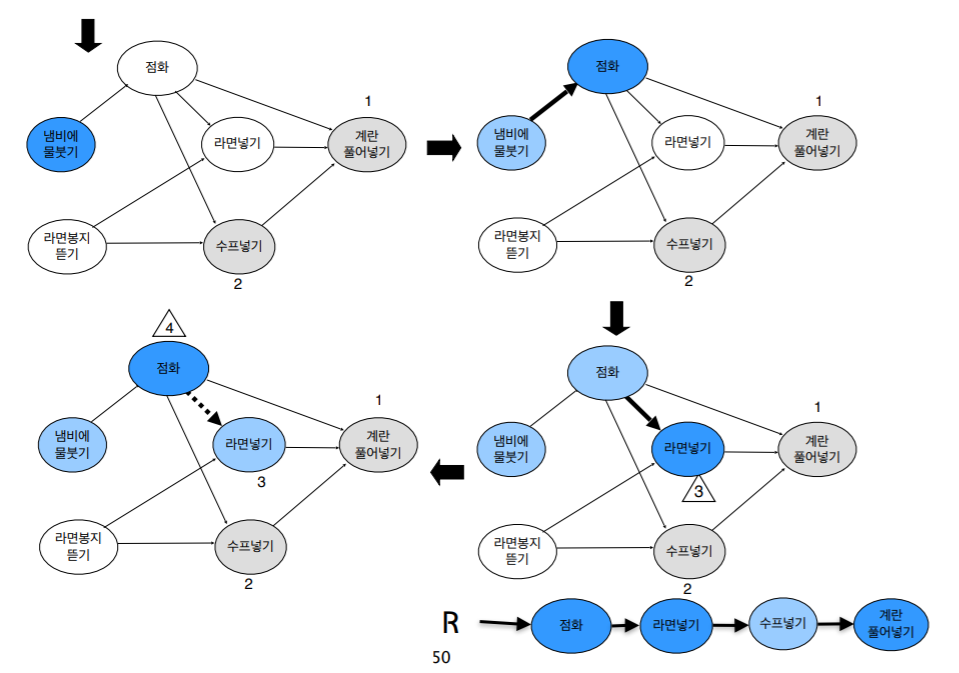
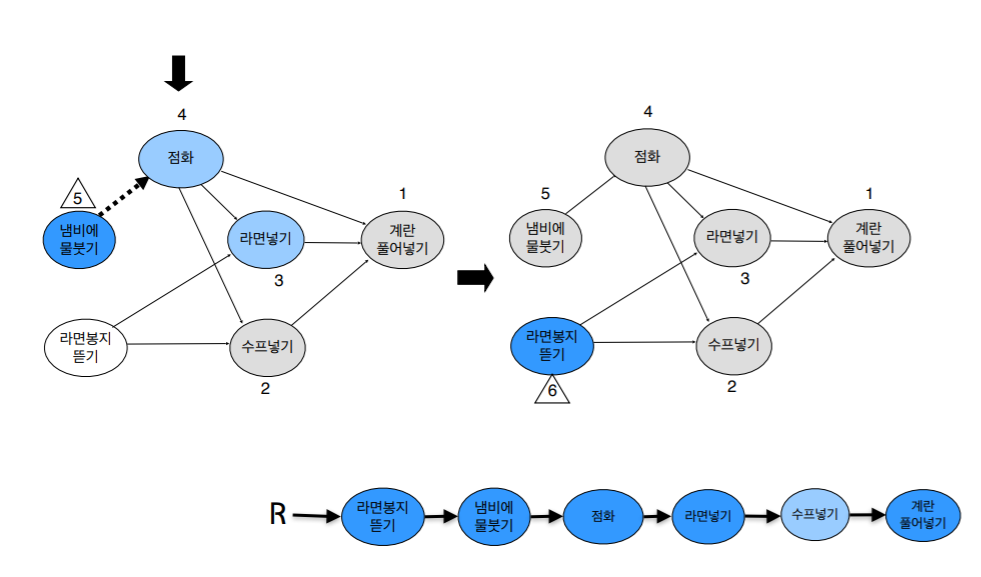
DFS-TS(v, R)
{
    visited[v] ← YES;
    for each x adjacent to v do
       if (visited[x] = NO) then
 			DFS-TS(x, R) ;
    add v at the front of the linked list R;
} 

• v 노드가 방문하지 않았다면 DFS-TS 호출
• v 노드를 방문표시
• v 노드 인접노드 x 들에 대해서 방문하지 않았다면 DFS-TS 재귀호출
• 인접노드가 없다면 v를 리스트 R의 가장 앞에 insert.
• 이렇게 재귀 방식으로 돌다가 최초 v로 돌아오면 다시 방문하지 않은 임의의 v 노드에 대해서 DFS-TS호출
• 알고리즘이 끝나면 연결 리스트 R에는 정점들이 위상정렬된 순서로 매달려 있다.
• 수행시간: Θ(n+m)