그래프

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

그래프

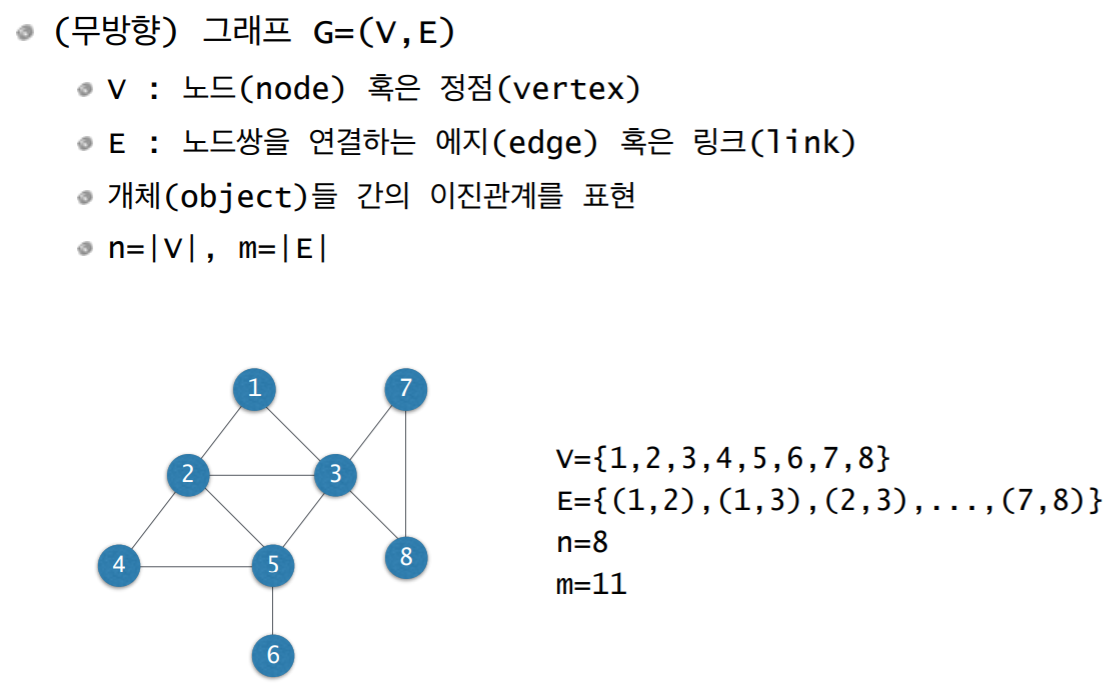
1. 그래프 (Graph)

• undirected graph라고도 한다.

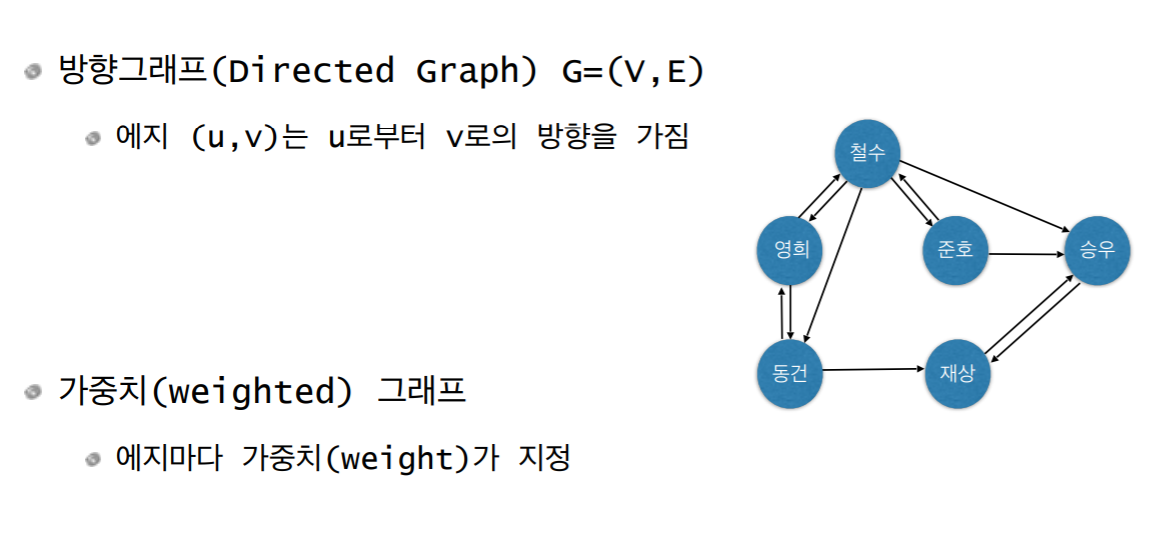
• directed graph는 (u, v)와 (v, u)가 서로 다를 때를 말한다.
• 위의 그림에서 철수에서 영희로 가는 방향(엣지), 영희에서 철수로 가는 방향가 서로 다르다고 정의 할 때

2. 그래프의 표현

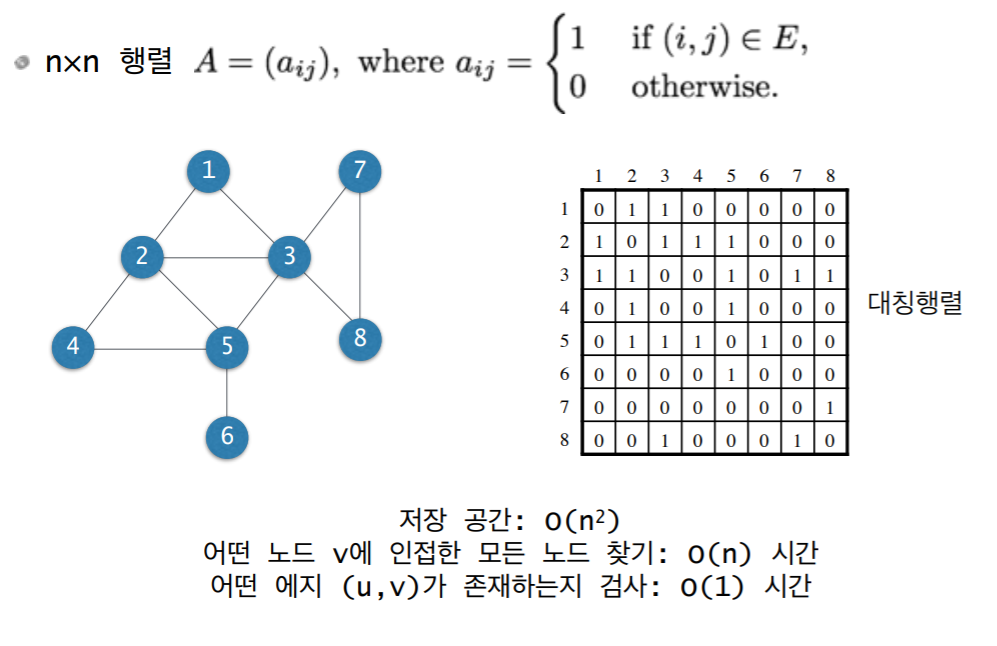
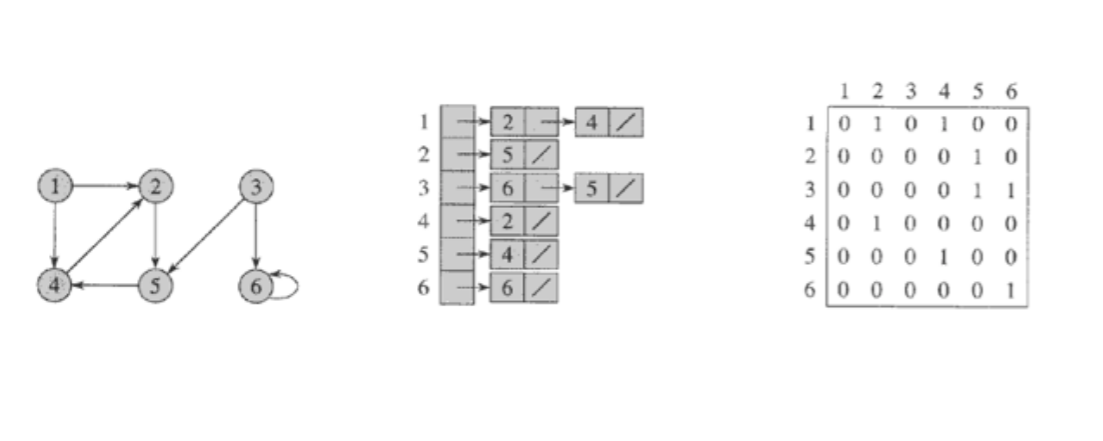
2.1 인접행렬 (adjacency matrix)

• (1, 2)의 값이 1, (2, 1)의 값도 1 서로 이렇게 (i, j ), (j, i) 값이 같다면 인접행렬이라고 한다.
• 어떤 노드에 인접한 모든 노드를 찾으려면 O (N) 시간이 걸린다. 왜냐하면 노드 3의 경우 인접한 노드가 1,2,5, 7, 8이다. 인접행렬에서 3행의 모든 열을 검색해야 한다.
• (U, V) 검색은 당연히 한 번만 검색하면 되기 때문에 O(1)

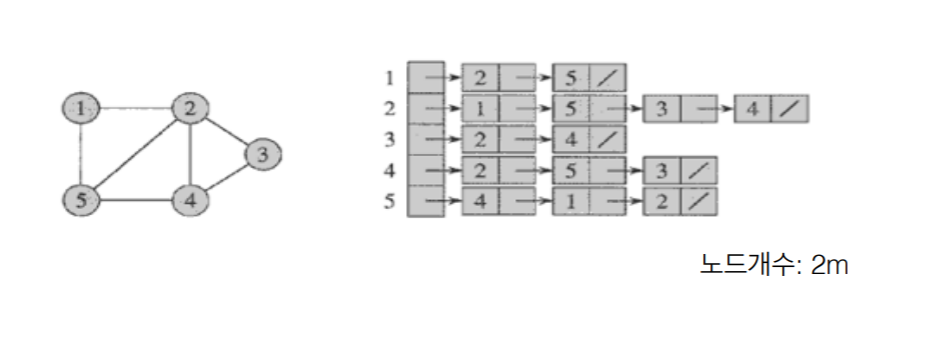
2.2 인접리스트 (adjacency list)

• 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들의 연결 리스트

• n은 노드의 개수

• m은 edge의 개수

• 리스트를 구성하는 총 노드의 개수가 2m인 이유는 인접한 노드들의 엣지가 양방향이므로 각 노드에 하나씩 있기 때문에. 예를 들어 노드 2를 보면 연결된 엣지들에 5가 있고 노드 5에는 엣지들에 2가 있기 때문에

• 저장 공간 O(n+m) : 원래는 O(n+ 2m)인데 표현에 의해서 이렇게

• 어떤 노드 v에 인접한 모든 노드 찾기 : O(degree(v)) 시간. 노드에 연결된 노드들만 검사하면 되는 시간. 물론 최악으로 한 노드가 모든 노드를 연결되어 있다면 n-1이 될 수 있음.
• 어떤 에지 (u, v)가 존재하는지 검사 : O(degree(u)) 시간. 노드 v인접 노드 찾기랑 같은 원리

2.3 방향 그래프

• 단방향 엣지만 있는 경우

• 자신을 가르키는 엣지도 있음

• 인접행렬은 비대칭
• 인접리스트는 m개의 노드를 가짐

3. 가중치 그래프의 인접행렬 표현

• 에지의 존재를 나타내는 값으로 1 대신 에지의 가중치를 저장
• 에지가 없을 때 혹은 대각선
  • 특별히 정해진 규칙은 없으며, 그래프와 가중치가 의미하는 바에 따라서
  • 예 : 가중치가 거리 혹은 비용을 의미하는 경우라면 에지가 없으면 무한대. 대각선은 0
  • 예 : 만약 가중치가 용량을 의미한다면 에지가 없을 때 0. 대각선은 무한대.
• 무한대라고 해서 우리가 아는 무한대가 아니라 그냥 가져다 쓰는 느낌. 가는 방향(에지)가 없다고 보자.
• 용량은 예를 들어서 노드 i에서 노드 j로 가는데 길이 3가지 or 10가지가 있다. 도시로 이야기하면 서울에서 대구까지는 길이 2개 대구에서 부산으로는 4개 이렇게 얘기할 때 4개가 하나의 엣지로 보는 것

4. 경로와 연결성

• 무향향 그래프로가 일단 가정하고 간다.
• 무방향 그래프 G=(V,E)에서 노드 u와 노드 v를 연결하는 경로(path)가 존재할 때 v와 u는 서로 연결되어 있다고 말함
• 노든 노드 쌍들이 서로 연결된 그래프를 연결된(connected) 그래프라고 한다.
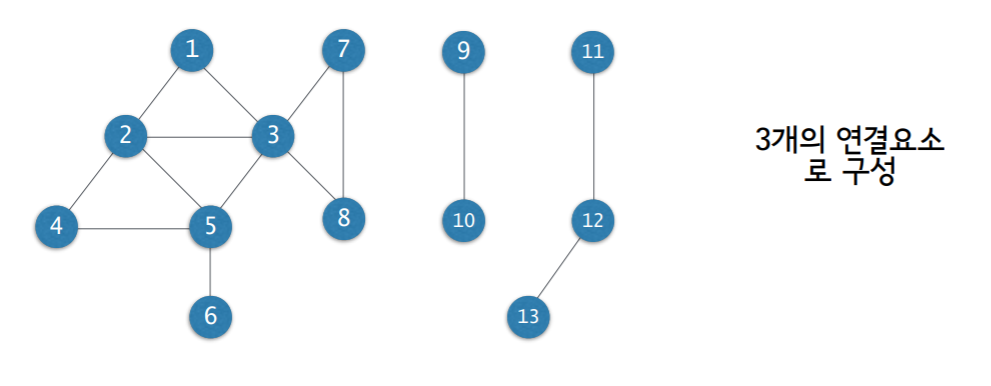
• 연결요소 (connected component)

• 위 그림에서는 3개의 연결 요소가 있다~ 라고 말할 수 있다.