해싱
Updated:
강의 사이트
- http://www.kocw.net/home/search/kemView.do?kemId=1148815
해싱
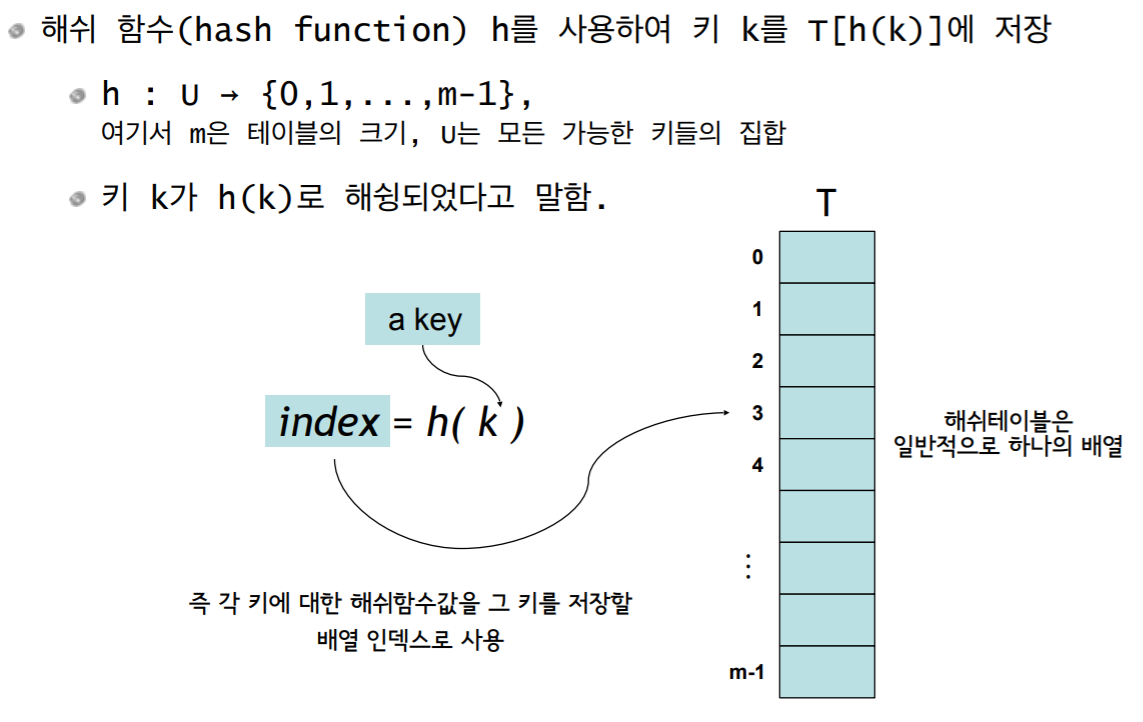
1. Hash Table
- 해쉬 테이블은 dynamic set을 구현하는 효과적인 방법의 하나
- 적절한 가정하에서 평균 탐색, 삽입, 삭제시간 O(1)
- 보통 최악의 경우 Θ(n)
2. 예
-
모든 키들을 자연수라고 가정. 어떤 데이터든지 자연수로 해석하는 것이 가능
- 예: 문자열
- ASCII 코드: C=67, L=76, R=82, S=83.
- 문자열 CLRS는 (67·128³)+(76·128²)+(82·128¹)+(83·128º)=141,764,947
- 해쉬 함수의 간단한 예:
- h(k) = k % m, 즉 key를 하나의 자연수로 해석한 후 테이블의 크기 m으로 나눈 나머지
- 항상 0~m-1 사이의 정수가 됨
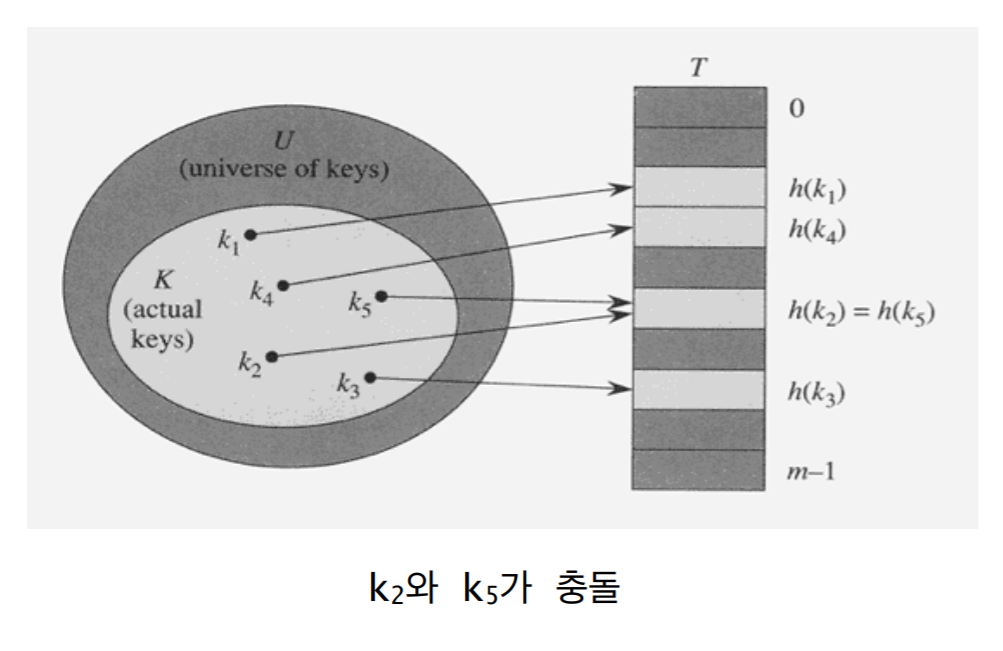
3. 충돌
- 두 개 이상의 키가 동일한 위치로 해슁되는 경우
- 즉, 서로 다른 두 키 k1과 k2에 대해서 h(k1)=h(k2)인 상황
-
일반적으로 U »m이므로 항상 발생 가능 (즉 단사함수가 아님) - 다시 말하면 실제 데이터들의 크기(U)는 저장될 크기 (m)보다 크거나 같을 수 밖에 없다. m은 제한 적이므로
- 충돌이 발생할 경우 대처 방법이 필요 대표적인 두 가지 충돌 해결 방법: chaining과 open addressing
4. Chaining에 의한 충돌 해결
- 동일한 장소로 해슁된 모든 키들을 하나의 연결리스트(Linked List) 로 저장
4.1 키의 삽입
- 키 K를 리스트 T[h(k)] 의 맨 앞에 삽입 : 시간복잡도 O(1)
- 중복된 키가 들어올 수 있고 중복 저장이 허용되지 않는다면 삽입시 리스트를 검색해야 함. 따라서 시간복잡도는 리스트의 길이에 비례
4.2 키의 검색
- 리스트 T[h(k)]에서 순차검색
- 시간복잡도는 키가 저장된 리스트의 길이에 비례.
4.3 키의 삭제
- 리스트 T[h(k)]로 부터 키를 검색 후 삭제
- 일단 키를 검색해서 찾은 후에는 O(1)시간에 삭제 가능
4.4 시간 복잡도
- 최악의 경우는 모든 키가 하나의 슬롯으로 해슁되는 경우
- 길이가 N인 하나의 연결리스트가 만들어짐
- 따라서 최악의 경우 탐색시간은 Θ(n)+해쉬함수 계산시간
- 평균시간복잡도는 키들이 여러 슬롯에 얼마나 잘 분배되느냐에 의해서 결 정
4.4.1 SHUA (Simple Uniform Hashing Assumption)
- 각각의 키가 모든 슬롯들에 균등한 확률로(eually likely) 독립적으로 (independently) 해슁된다는 가정
- 성능분석을 위해서 주로 하는 가정임
- hash함수는 deterministic하므로 현실에서는 불가능
- 즉, 현실에서는 불가능한 가정이지만 단순히 성능을 분석하기 위한 가정이다.
- Load factor α = n/m:
- n: 테이블에 저장될 키의 개수.
- m: 해쉬테이블의 크기, 즉 연결리스트의 개수
- 각 슬롯에 저장된 키의 평균 개수
- 연결리스트 T[j]의 길이를 nj라고 하면 E[nj] = α
-
만약 n=O(m)이면 평균검색시간은 O(1)
-
내가 이해한 내용 : 그니까 데이터들의 키가 테이블의 각 슬롯에 균등하게 해슁된다고 가정하자. 그리고 Load factor는 각 슬롯에 저장된 키의 평균 개수 즉, 테이블에 저장될 총 각 데이터 키의 개수를 키가 저장될 해쉬 테이블의 크기로 나누면 테이블의 슬롯에 저장될 키의 평균 개수가 나온다.
이때 T[j] (한 슬롯의 연결리스트 길이)의 길이를 nj라고 한다면E[nj] = α 인데, 처음 가정한대로 각 슬롯에 키가 균등하게 해슁된다고 했으니 n=O(m)라고 말할 수 있다. 따라서 n /m =1이고 α = n/m이므로 그러면 O(α) = O(1)이 된다.
5. Open Addressing에 의한 충돌 해결
- 모든 키를 해쉬 테이블 자체에 저장
- 테이블의 각 칸(slot)에는 1개의 키만 저장
- 충돌 해결 기법
- Linear probing
- Quadratic probing
- Double hashing
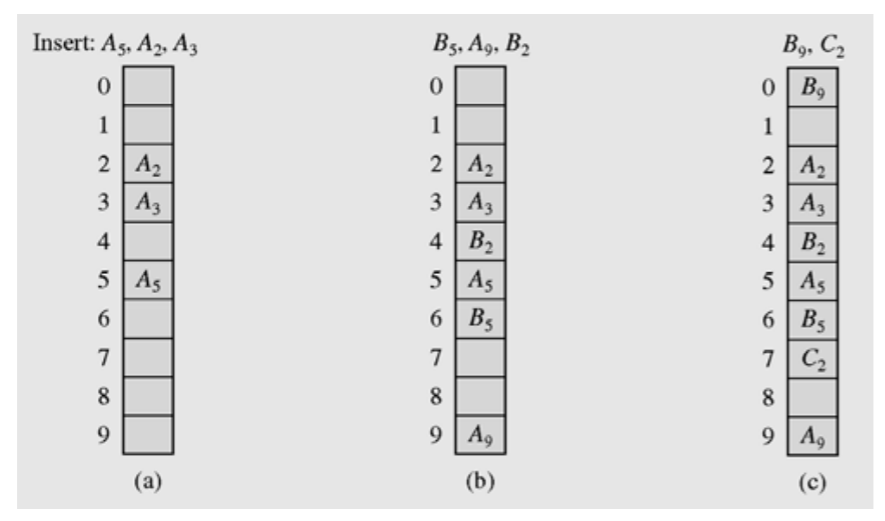
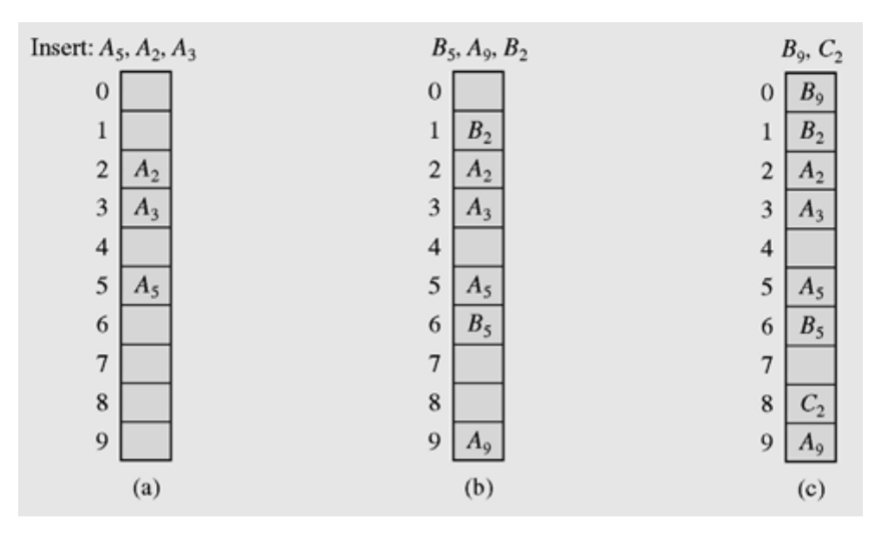
5.1 Linear probing
- h(k), h(k)+1, h(k)+2,… 순서로 검사하여 처음으로 빈 슬롯에 저장 테이블의 끝에 도달하면 다시 처음으로 circular하게 돌아감
5.1.1 단점
-
primary cluster: 키에 의해서 채워진 연속된 슬롯들을 의미
-
이런 cluster가 생성되면 이 cluster는 점점 더 커지는 경향이 생김
5.2 Quadratic probing
- 충돌 발생시 h(k), h(k)+1^2, h(k)+2^2, h(k)+3^2 ,… 순서로 시도
5.3 Double hashing
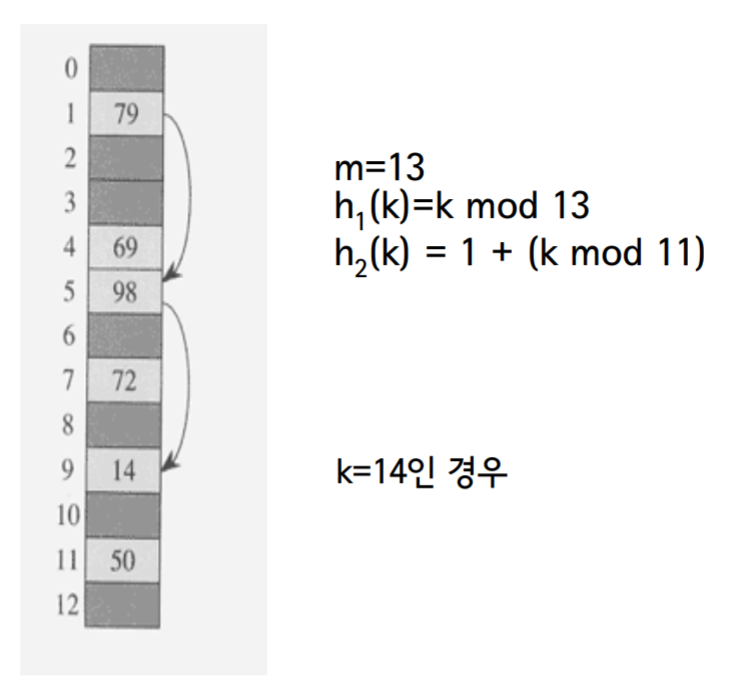
- 서로 다른 두 해쉬 함수 h1과 h2를 이용하여 h(k,i) = (h1(k) + i·h2(k)) mod m
- 배열의 크기가 13이라고 가정. 13으로 나눈다.
- K=14일 경우 처음 h1에 넣는다 그럼 14를 13으로 나눈 나머지 h1(14)의 값은 1이다.
- 그리고 h2(14)의 경우 1+ (14 mod 11)이므로 4이다.
- 처음 h1에서 나온 값 1로 1번 슬롯을 보자. 있으면 넣으면 됨. 그러나 여기선 79가 있으므로 패스
- 그럼 1과 h2에서 나온 값인 4를 더해서 5번 슬롯을 보자. 이번에도 98이 있다.
- 그럼 다시 5에 h2 값인 4를 더해서 9번 슬롯을 보면 비어 있으므로 14번을 넣는다.
- 즉, h1에서 나온 값의 슬롯이 비어 있다면 넣으면 되지만 없다면 h2에 나온 값을 계속 더해간다. 더해서 테이블의 크기보다 커지면 다시 테이블의 크기만큼 나누면 된다.
6. 키의 삭제
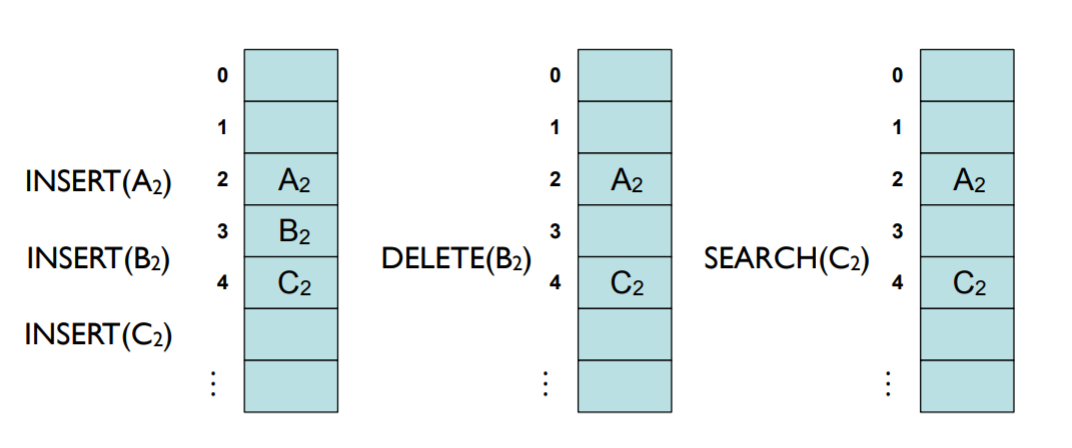
- 단순히 키를 삭제할 경우 문제가 발생
- 가령 A2, B2, C2가 순서대로 모두 동일한 해쉬함수값을 가져서 linear probing으로 충돌 해결한다고 가정
-
그리고 B2를 삭제했다고 가정
- 이때 C2를 검색한다면 A2를 검색하고 B2를 지나 C2를 가야하는데 B2가 없음. 그럼 뒤에는 없다고 생각.
- 그래서 B2가 삭제 될때 delete 표시를 해줌.
- 그럼 또 문제가 발생. delete가 많아지면 모든 칸들이 delete로 채워짐.
- 그럼 테이블 전체를 검색할 수 밖에 없어짐.
- 그래서 B2가 삭제될 때 C2를 B2자리로 옮겨놔야 함.
7. 좋은 해쉬 함수란?
- 현실에서는 키들이 랜덤하지 않음
- 만약 키들의 통계적 분포에 대해 알고 있다면 이를 이용해서 해쉬 함수를 고 안하는 것이 가능하겠지만 현실적으로 어려움
- 키들이 어떤 특정한 (가시적인) 패턴을 가지더라도 해쉬함수값이 불규칙적이 되도록 하는게 바람직
- 해쉬함수값이 키의 특정 부분에 의해서만 결정되지 않아야
7.1 Division 기법
-
h(k) = k mod m
-
예 : m = 20 and k = 91 => h(k) = 11
-
장점 : 한 번의 mod 연산으로 계산. 따라서 빠름
-
단점 : 어떤 m 값에 대해서는 해쉬 함수 값이 키값의 특정 부분에 의해서 결정되는 경우가 있음
가령 m= 2 ^ p 이면 키의 하위 비트가 해쉬 함수 값이 됨
7.2 Multiplication 기법
- 0에서 1사이의 상수 A를 선택: 0 0 < A < 1
- kA의 소수부분만을 택한다.
-
소수 부분에 m을 곱한 후 소수점 아래를 버린다.
- 예: m=8, word size = w = 5, k = 21.
- A = 13/32를 선택 kA = 21⋅13/32 = 273/32 = 8 + 17/32
- m (kA mod 1) = 8 · 17/32 = 17/4 = 4.···
- 즉, h(21) = 4
- 꼭 이렇게 하라는 것이 아닌 해쉬의 성능을 올리기 위한 키 값들이 불규칙하게 만들기 위해서 이렇게 복잡하게 쓴다~ 라는 이야기
8. JAVA에서의 Hash Code
- Java의 Object 클래스는 hashCode() 메서드를 가짐.
- 따라서 모든 클 래스는 hashCode() 메서드를 상속받는다.
- 이 메서드는 하나의 32비트 정수를 반환한다.
- 만약 x.equals(y)이면 x.hashCode()==y.hashCode()이다. 하지만 역은 성립하지 않는다.
- Object 클래스의 hashCode() 메서드는 객체의 메모리 주소를 반환하는 것으로 알려져 있음 (but it’s implementation-dependent.) 강사 생각 : 공식적인 자바의 문서에는 없다고 함.
- 필요에 따라 각 클래스마다 이 메서드를 override하여 사용한다.
- 예: Integer 클래스는 정수값을 hashCode로 사용
- hashCode() for Strings in Java 예시
public final class String
{
private final char[] s;
…
public int hashCode()
{
int hash = 0;
for (int i = 0; i < length(); i++)
hash = s[i] + (31 * hash);
return hash;
}
}
- 사용자 정의 클래스의 예
public class Record
{
private String name;
private int id;
private double value;
…
public int hashCode() {
int hash = 17; // nonzero constant
hash = 31*hash + name.hashCode();
hash = 31*hash + Integer.valueOf(id).hashCode();
hash = 31*hash + Double.valueOf(value).hashCode();
return hash;
}
}
//모든 멤버들을 사용하여 hashCode를 생성한다.
8.1 hashCode와 hash 함수
- Hash code: -2 ^ 31에서 2 ^ 31사이의 정수
- Hash 함수: 0에서 M-1까지의 정수 (배열 인덱스)
private int hash(Key key){
return (key.hashCode() & 0x7fffffff) % M;
}
8.2 HashMap
-
4장에서 다룬 TreeMap 클래스와 유사한 인터페이스를 제공 (둘 다 java.util.Map 인터페이스를 구현)
- 내부적으로 하나의 배열을 해쉬 테이블로 사용
- 해쉬 함수는 8.1의 hash 함수와 유사함
- chaining으로 충돌 해결
- load factor를 지정할 수 있음 (0~1 사이의 실수)
- 저장된 키의 개수가 load factor를 초과하면 더 큰 배열을 할당하고 저장된 키들을 재배치(re-hashing)
8.3 HashSet
HashSet<MyKey> set = new HashSet<MyKey>();
set.add(MyKey);
if (set.contains(theKey))
…
int k = set.size();
set.remove(theKey);
Iterator<MyKey> it = set.iterator();
while (it.hasNext()) {
MyKey key = it.next();
if (key.equals(aKey))
it.remove();
}