감 1도 없는 개발자

감 1도 없는 개발자

여행을 꿈꾸는 개발자

red black tree

Updated:

강의 사이트
  • http://www.kocw.net/home/search/kemView.do?kemId=1148815

Red black tree

1. Red black tree

  • 이진 탐색 트리의 일종, 변형
  • 균형잡힌 트리 : 높이가 O(log2N)
  • 탐색, 삽입, 삭제 연산을 최악의 경우에도 O(log2N) 시간

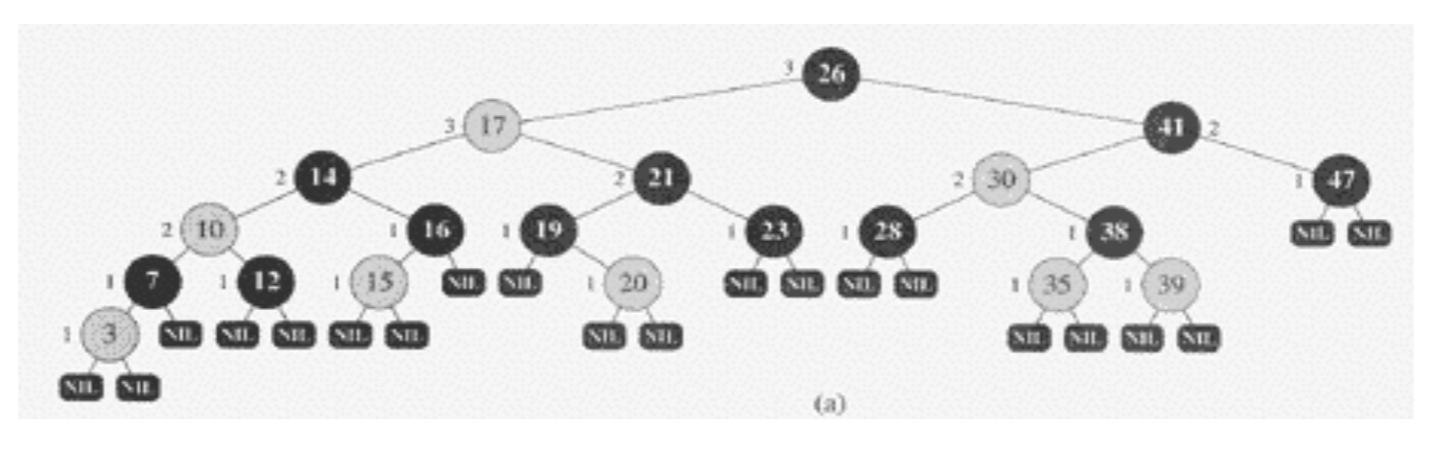
  • 각 노드는 하나의 키(key), 왼쪽자식(left), 오른쪽 자식(right), 그리고 부모노드(p)의 주소를 저장

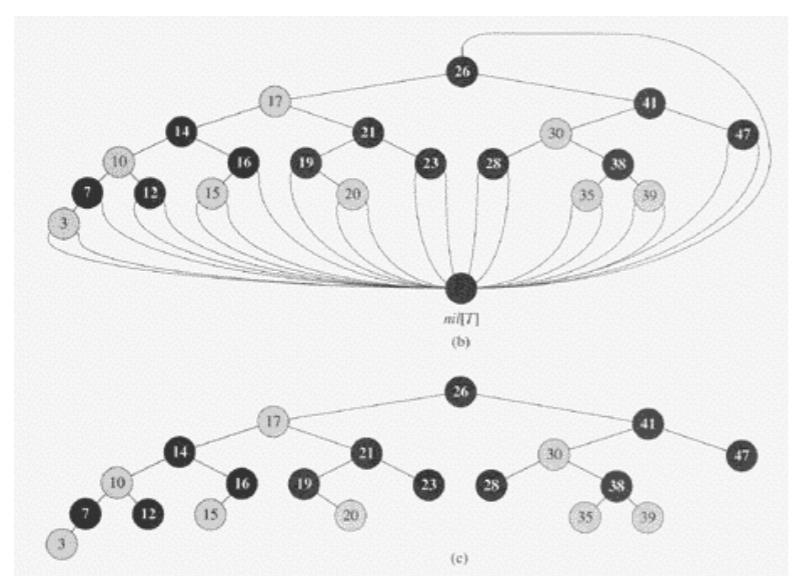
  • 자식노드가 존재하지 않을 경우 NIL 노드라고 부르는 특수한 노드가 있다고 가정
  • 따라서 모든 리프노드는 NIL노드
  • 루트의 부모도 NIL노드라고 가정
  • 노드들은 내부노드와 NIL노드로 분류
  • NIL 노드는 설명하기 위해서 사용하는 것. 실제 구현할 때는 없음.

2. 정의

  1. 각 노드는 red 혹은 black이고,
  2. 루트노드는 black이고,
  3. 모든 리프노드(즉, NIL노드)는 black이고,
  4. red노드의 자식노드들은 전부 black이고 (즉, red노드는 연속되어 등장하 지 않고),
  5. 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다. (black -height 문제라고 불림)

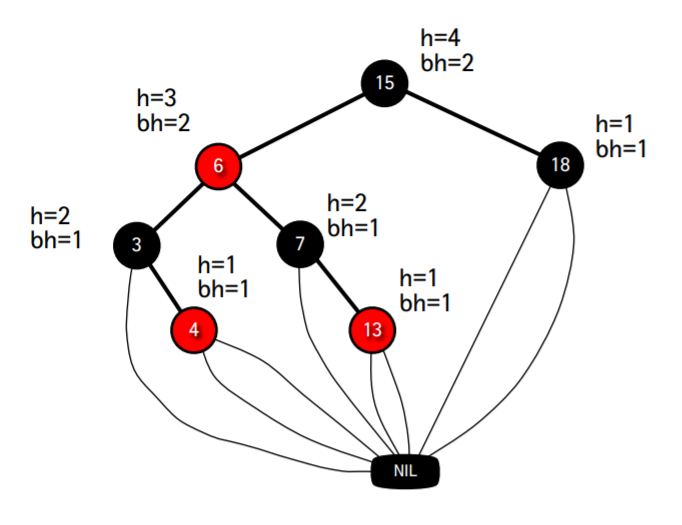
3. 높이

  • 노드 x의 높이 h(x)는 자신으로부터 리프노드까지의 가장 긴 경로에 포함된 에지의 개수이다.
  • 노드 x의 블랙-높이 bh(x)는 x로부터 리프노드까지의 경로상의 블랙노드의 개수이다 (노드 x 자신은 불포함)

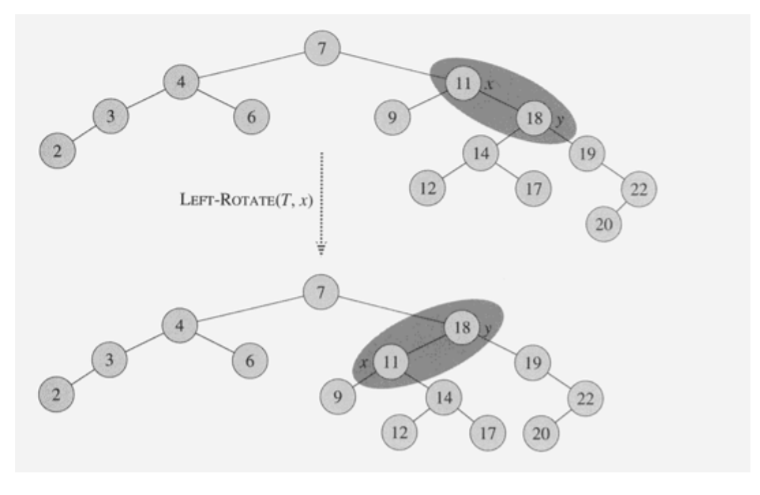
4. Left and Right Rotation

  • 탐색은 기존의 이진 트리 탐색이랑 차이가 없다.

  • INSERT와 DELETE 가 차이가 있는데 이를 위해 Rotation을 알아야 한다.

  • 시간복잡도 O(1)
  • 이진탐색트리의 특성을 유지

  • X, Y를 서로 left, rigth rotation하는 예제

4.1 Pseudo Code

5. INSERT

  • 새로 넣은 노드 Z는 무조건 RED로 한다.
  • 이때 부모 노드인 Y가 RED이면 RED-BLACK 조건이 위반된다.

5.1 위반조건

  1. 각 노드는 RED OR BLACK
    • 일단 상관 없음 PASS
  2. 루트 노드는 BLACK이다
    • 들어온 Z가 ROOT였다면 문제가 발생. (RB-INSERT-FIXUP 메소드에서 해결)
  3. 모든 리프 노드(즉, NIL 노드)는 BLACK
    • Z는 리프노드가 아니므로 상관 없음
  4. RED 노드의 자식 노드들은 전부 BLACK이어야 한다.
    • 이게 가장 큰 문제이다. (RB-INSERT-FIXUP 메소드에서 해결)
  5. 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
    • 이것도 RED로 처음 만들기 때문에 상관 없다.

5.2 RB-INSERT-FIXUP

  • Loop Invariant
    • Z는 새로 INSERT되면서 RED 노드로 설정
    • 오직 하나의 위반만이 존재한다.
    • 위반 조건 2 : Z가 루트 노드이면서 RED이다.
    • 위반 조건 4 : Z와 그 부모 p[Z]가 둘다 RED인 경우
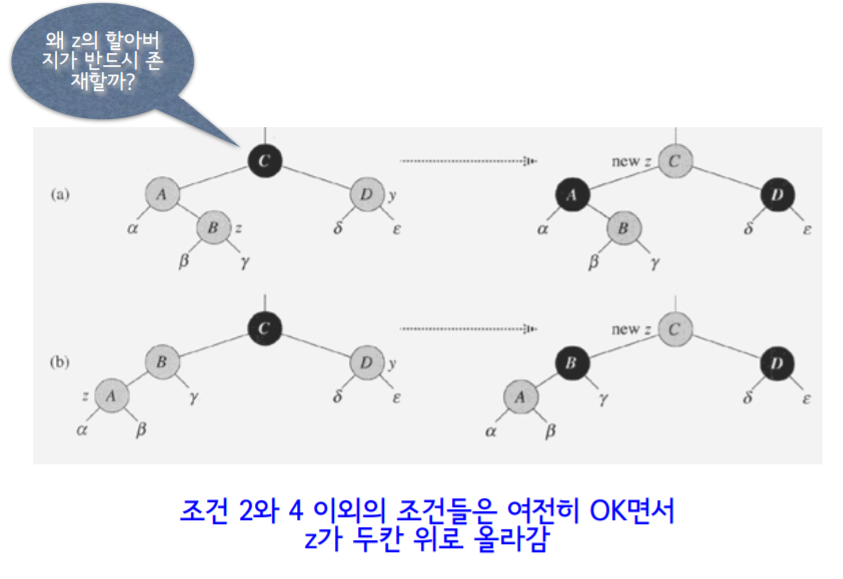
  • 기본 해결책 : 위반 조건 4에서 부모 노드를 p[z]를 Black으로 변경. 그리고 위에 할아버지 노드가 black이었다면 RED로 변경. 그렇다면 할아버지의 할아버지랑 문제가 발생. Z를 할아버지로 바꾸고 다시 RB-INSERT 메소드로 해결. 그렇게 Z가 ROOT 노드 까지 갔는데 ROOT가 RED가 된다면 단순히 BLACK으로 바꾸면 됨.
5.2.1 Z의 삼촌이 RED인 경우
  • 경우 1 : Z의 삼촌이 RED인 경우

  • RB-INSERT-FIXUP의 기본 해결책으로 해결 가능
5.2.2 Z의 삼촌이 BLACK인 경우

  • 그림의 C 노드 오른쪽 노드를 델타(NIL)로 한 이유는 NIL 노드일 경우도 있을 수 있음. (우리가 처음 배울때 NIL노드도 BLACK이라고 가정하고 들어감.)
  • 따라서 C 노드의 오른쪽 노드가 BLACK라는 가정에서 노드가 있다고 해도 BLACK ,없다고 해도 NIL이므로 BLACK이다. 이때!!
  1. 경우 2: Z가 부모의 오른쪽 자식인 경우
    • p[z]에 대해서 left rotation한 후 z를 p[z]로 바꾼다. 그리고 경우 3으로 간다.
  2. 경우 3: Z가 부모의 왼쪽 자식인 경우
    • p[z]를 black으로, p[p[z]]를 RED로 바꾼다.
    • p[[z]]에 대해서 right-rotation을 진행
5.2.3 경우 4,5,6
  • 경우 1,2,3은 p[z]가 p[p[z]]의 왼쪽자식인 경우들
  • 경우 4,5,6은 p[z]가 p[p[z]]의 오른쪽 자식인 경우: 경우 1,2,3과 대칭적
  • 경우들은 서로 왔다 갔다 할 수 있다. 경우 1에서 경우 4로 갈 수도 있음.
  • 결국 서로 경우를 왔다 갔다 하다가 root에 도착해서 끝

5.3 Pseudo Code

  • BST에서의 INSERT: O(log2n)
  • RB-INSERT-FIXUP
    • 경우1에 해당할 경우 z가 2레벨 상승
    • 경우 2,3에 해당할 경우 O(1)
    • 따라서 트리의 높이에 비례하는 시간
  • 즉, INSERT의 시간복잡도는 O(log2n)

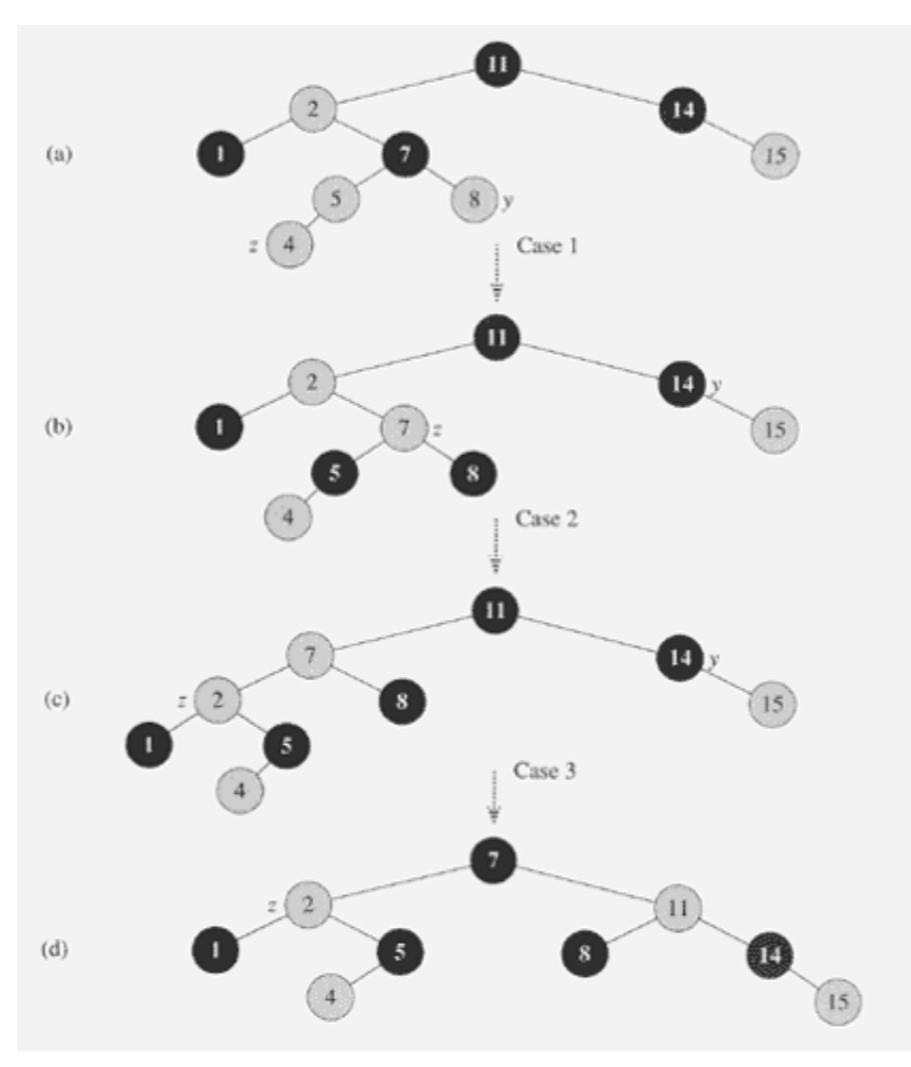
5.4 예제

6. DELETE

  • successor : 자신의 노드보다 큰 노드 중 에서 가장 작은 노드

6.1 RB-DELETE-FIXUP(T, X)

  1. 각 노드는 RED OR BLACK
    • 일단 상관 없음 PASS
  2. 루트 노드는 BLACK이다
    • 루트가 삭제되고 올라온 노드가 RED라면 BLACK으로 바꾸면 됨
  3. 모든 리프 노드(즉, NIL 노드)는 BLACK
    • 상관 없음 PASS
  4. RED 노드의 자식 노드들은 전부 BLACK이어야 한다.
    • y가 삭제되는데 p[y]와 x(y의 자식)가 모두 red일 경우 그냥 p[y]를 black으로 하면됨. 2번과 동일
  5. 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
    • 삭제할 노드가 red면 상관이 없다.
    • 그러나 black일 경우 5번 조건에 위반. 삭제할 노드 Y가 부모 노드인 p[y]의 오른쪽 자식이라면, 해당 길이 p[y]의 왼쪽 자식으로 가는 길에 만날 black 노드보다 하나 줄어드는 상황이 된다.
    • 5번을 해결하기 위해 RB-DELETE-FIXUP 메소드를 사용
    • 노드 x에 “extra black”을 부여해서 일단 조건5를 만족
    • 노드 x는 “double black” 혹은 “red & black”

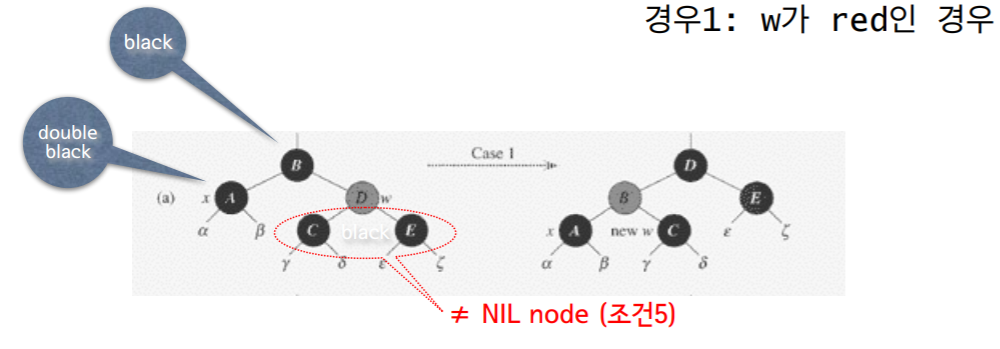
6.2 경우 1: W가 RED인 경우

  • 경우 1,2,3,4 : X가 부모의 왼쪽
  • 경우 5,6,7,8 : X가 부모의 오른쪽
  • 따라서 1,2,3,4만 알면 5,6,7,8은 대칭점

  • w의 자식들은 black
  • w를 black으로, p[x]를 red로
  • p[x]에 대해서 left-rotation적용
  • x의 새로운 형제노드는 원래 w의 자식노드, 따라서 black 노드
  • 경우 2,3, 혹은 4에 해당

아 XX 일단 포기… 강사도 헷갈린다는데 뭘. 알고리즘을 안다고 해서 술술 가는게 아니라 경우의 수마다 INSERT, DELETE가 다름. 일단 다른 강의를 보고 나중에 쭉 본다음 다시 봐야겠다.

You may also enjoy