이진검색트리

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

이진 검색 트리(Binary Search Tree)

1. Dynamic Set

2. 다양한 방법들

• 정렬된 혹은 정렬되지 않은 배열 혹은 연결 리스트를 사용할 경우 INSERT, SEARCH, DELETE 중 적어도 하나는 O(n)
• 이진탐색트리(Binary Search Tree), 레드-블랙 트리, AVL-트리 등의 트리에 기반한 구조들
• Direct Address Table, 해쉬 테이블 등

3. 검색 트리

• Dynamic set을 트리의 형태로 구현
• 일반적으로 SEARCH, INSERT, DELETE 연산이 트리의 높이 (height)에 비례하는 시간복잡도를 가짐
• 이진검색트리(Binary Search Tree), 레드-블랙 트리(red-black tree), B-트리 등

4. 이진 검색 트리(BST)

• 이진 트리이면서
• 각 노드에 하나의 키를 저장
• 각 노드 v에 대해서 그 노드의 왼쪽 부트리(subtree)에 있는 키들은 key[v]보다 작거나 같고, 오른쪽 부트리에 있는 값은 크거나 같다.

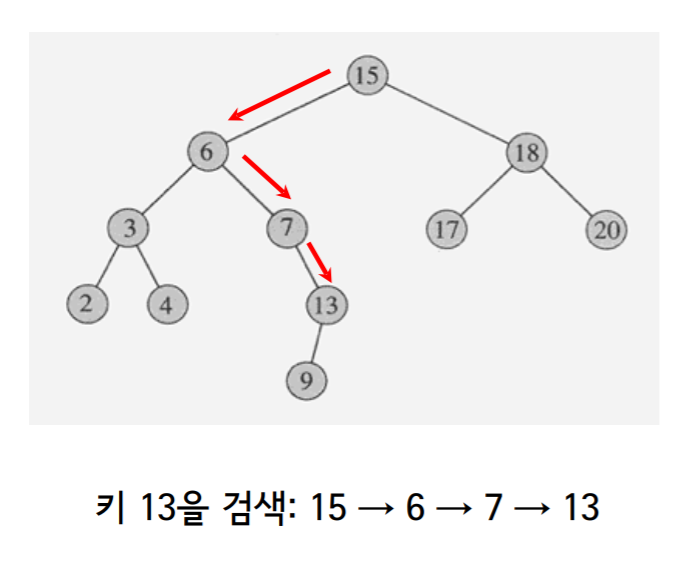
4.1 SEARCH

• 재귀 함수로

• 반복문으로

4.2 최대 값, 최소 값

• 최소 값은 항상 왼쪽 부트리에 존재
• 최대 값은 항상 오른쪽 부트리에 존재

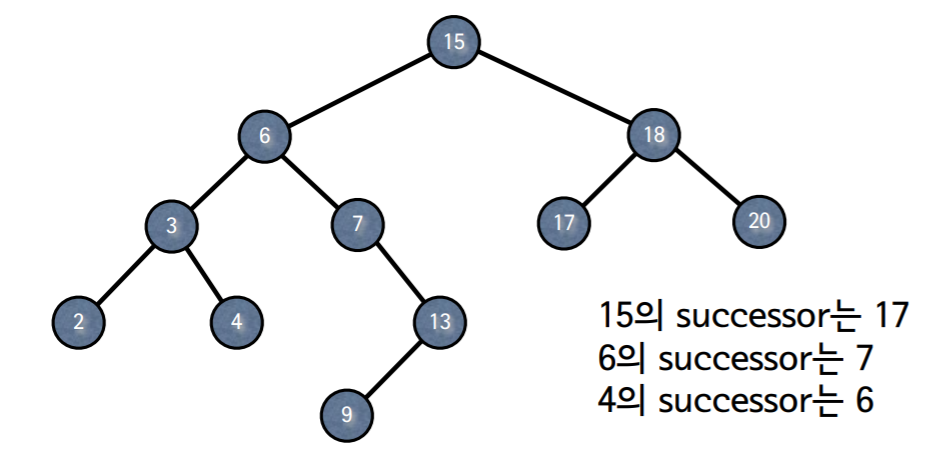
4.3 Successor

• 노드 x의 successor란 key[x]보다 크면서 가장 작은 키를 가진 노드
• 모든 키들이 서로 다르다고 가정

4.3.1 Successor 3가지 경우

1. 노드 x의 오른쪽 부트리가 존재할 경우, 오른쪽 부트리의 최소값.

2. 오른쪽 부트리가 없는 경우, 어떤 노드 y의 왼쪽 부트리의 최대값이 x가 되는 노드 y가 x의 successor.
   • 부모를 따라 루트까지 올라가면서 처음으로 누군가의 왼쪽 자식이 되는 노드
3. 그런 노드(2번) y가 존재하지 않을 경우 successor가 존재하지 않음 (즉, x가 최대값)

4.4 PredeCessor

• 노드 x의 predecessor란 key[x]보다 작으면서 가장 큰 키를 가진 노드
• Successor와 반대

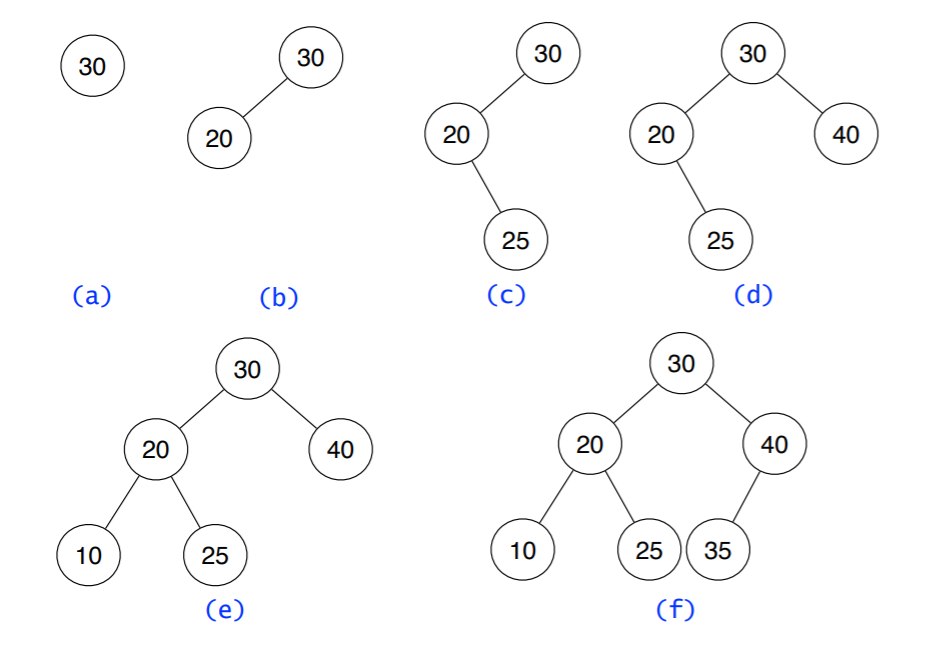
4.5 INSERT

4.6 DELETE

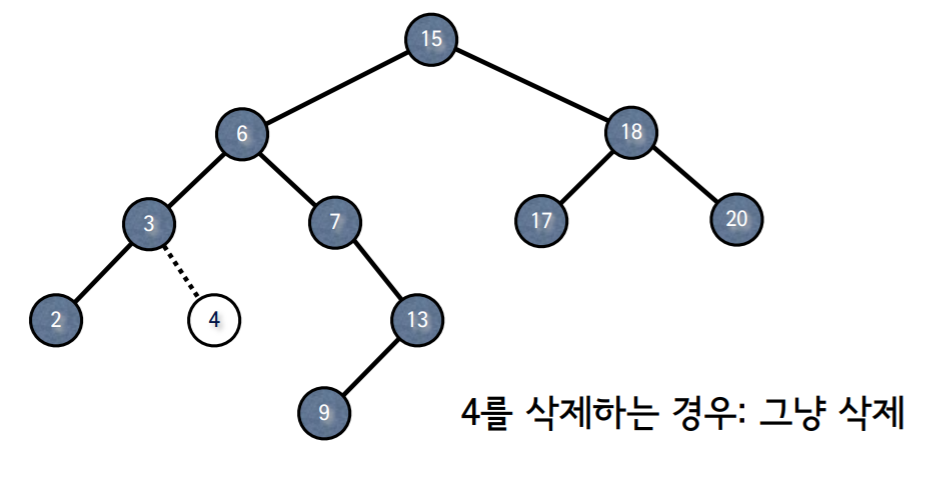
4.6.1 자식 노드가 없는 경우

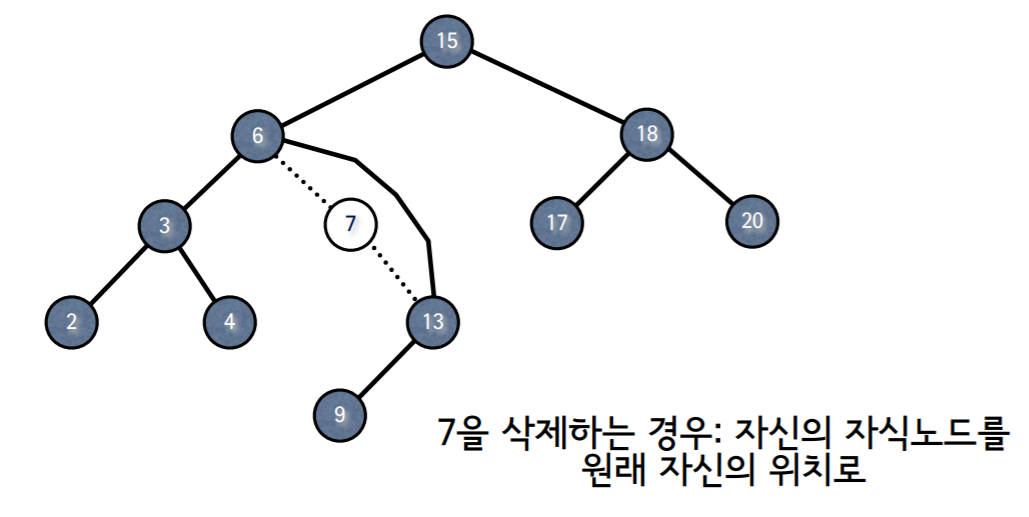
4.6.2 자식 노드가 1개인 경우

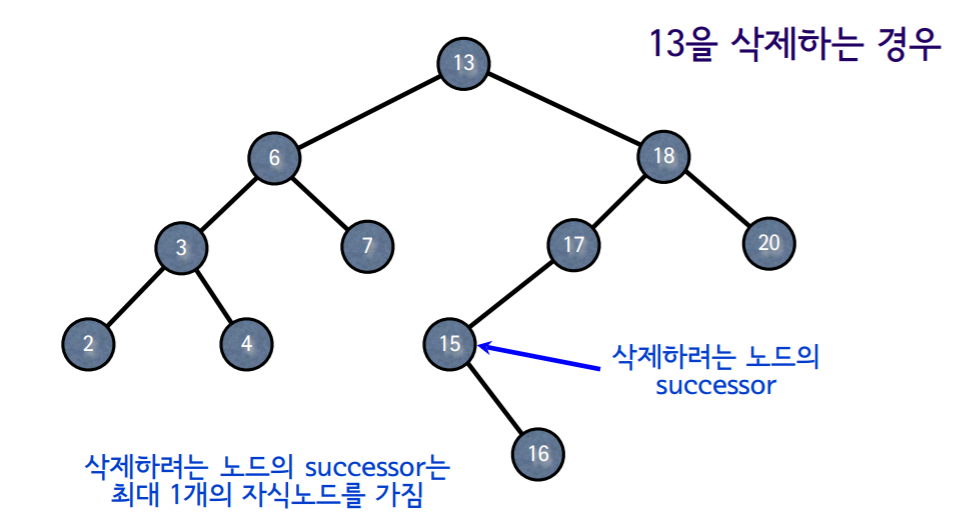
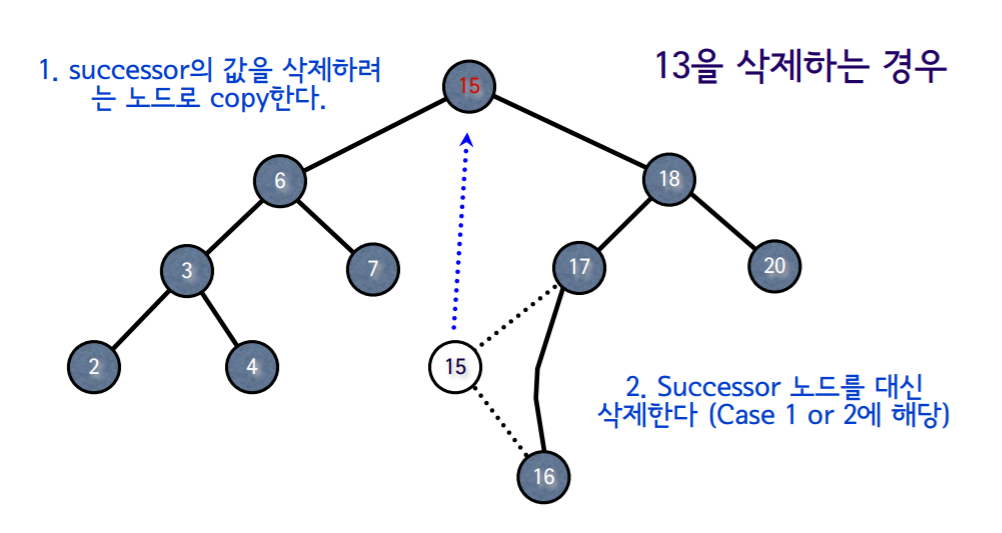
4.6.3 자식노드가 2개인 경우

5. 정리

• 각종 연산의 시간복잡도 O(h)
• 그러나, 최악의 경우 트리의 높이 h=O(n)
• 균형잡힌(balanced) 트리 레드-블랙 트리 등 키의 삽입이나 삭제시 추가로 트리의 균형을 잡아줌으로써 높이를 O(log2n) 으로 유지