선형시간 정렬 알고리즘(기수정렬)

강의 사이트

• http://www.kocw.net/home/search/kemView.do?kemId=1148815

선형시간 정렬 알고리즘(기수정렬)

• N개의 d자리 정수들이라고 가정한다. (꼭 정수라는 게 아니라 Radix 정렬 알고리즘을 보여 주기 위한 하나의 예)
• 가장 낮은 자리수부터 정렬한다고 가정한다. (Radix Sort)
• 가장 높은 자리수부터 정렬하는 것이 Bucket Sort라고 한다.
• 계수 정렬을 이용한다.

1. Radix Sort (기수 정렬)

• 일의 자리를 먼저 비교한다. 그에 맞추어서 정렬한다.
• 이번에는 십의 자리를 비교한다. 그에 맞추어서 정렬한다.
• 이번에는 백의 자리를 비교한다. 그에 맞추어서 정렬한다.

• 그런데 이렇게 했는데 어떻게 정렬이 되는가?

• Radix Sort 정렬은 stable 정렬 알고리즘이기 때문이다.
• stable은 무엇인가? 비교하는 데이터가 같을 경우 먼저 탐색(입력)된 데이터가 먼저 출력 되기 때문이다.
• 즉, 일의 자리에서 먼저 정렬되었기 때문에, 십의 자리로 정려할 경우 십의 자리가 같다면 먼저 정렬되어 있던 일의 자리 때문에 작은 수가 큰수보다 앞에 나오게 되어 있다.
• 예를 들어 처음 일의 자리를 가지고 정렬을 했다고 가정하자.
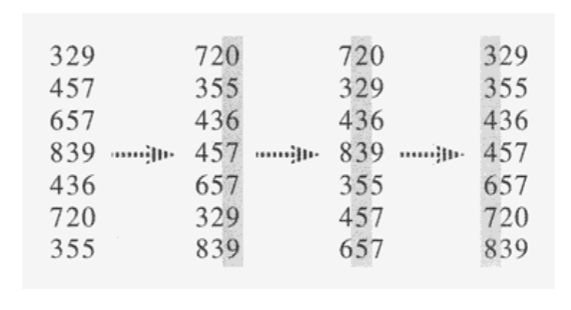
• 그렇다면 그림에서 왼쪽 두번째 숫자들을 보면 720, 355, 436으로 되어 있다.
• 다음 십의 자리로 정렬하면 그림에서 왼쪽부터 세번째 숫자들처럼 720, 329, 436이 되어있다.
• 이때 백의 자리를 빼고 생각하면 20, 29, 36이다. 당연히 20이 29보다 앞에 와야 한다.
• 다시 돌아가서 그림의 왼쪽에서 두 번째 숫자들을 보면 720이 329보다 위에 있다. 이미 일의 자리로 stable하게 정렬되어 있었기 때문에 720이 먼저 탐색(입력)된 숫자이므로 329보다 720이 앞에 위치 한다.

1.1 Pseudo Code & 시간복잡도

• O(D X (N + K))
• D는 숫자의 자릿수
• N은 숫자의 개수(즉, 데이터 갯수)
• K는 데이터가 가질 수의 서로 다른 갯수 (위의 예제에서는 10라고 보면 될듯. 각 자리 수 마다 0부터 9까지 가질 수 있으니까)

1.2 구현

• 위의 그림 예제는 모두 3자리 수였으나 실제와 같이 데이터가 자리 수 상관 없이 있다고 가정하에 구현

public class RadixSort {
	public static void main(String[] args) {
		int[] array=  { 142, 243, 21, 13, 11,7, 86 };
		int[] sort = radixSort(array);

		System.out.print("최종정렬 : ");
		printArray(sort);
	}
	
	private static int[] radixSort(int[] arr) {
		
		int max = getMax(arr); // arr의 최대값을 구한다.
		
		//최대값의 자리수 만큼 반복 수도 코드에서 D라고 보면 된다.
		for(int i = 0; i < (int)Math.log10(max) + 1; i++) {
			arr = linerSort(arr, (int)(Math.pow(10, i)));
			//각 자릿수 기준으로 정렬(계수정렬)
			System.out.print((int)Math.pow(10, i) + "자리로 정렬 : ");
			printArray(arr);
		}
		
		return arr;
	}
	
	static int getMax(int[] data) {
		int mx = data[0];
		for(int i=1; i<data.length; i++) {
			if(data[i] > mx) {
				mx = data[i];
			}
		}
		return mx;
	}
	
	private static int[] linerSort(int[] arr, int k) {
		//k는 arr 데이터들 중 최대값의 자릿수이다.
		int[] sort = new int[arr.length];
		// 어떤 자리수이든 0~9까지 밖에 없으니 누적 가운트 배열 크기는 10이다.
		int[] count = new int[10];
		
		// arr의 수들에 대해서 K의 자리수를 counting 한다.
		for(int i = 0; i < sort.length; i++) {
			count[(arr[i]/k)%10]++;
			/* K가 10일 경우(즉, 10의 자리를 가지고 비교할 경우)
			 * 예로 123일 때 2를 뽑아 내야한다. 따라서 arr[i]를 10으로 나누고
			 * %10을 하면 2가 나온다.
			 */
		}
		
		// 카운팅한 배열 count를 누적 카운트로 바꾼다.
		for(int i = 1; i < count.length; i++) {
			count[i] = count[i-1] + count[i];
		}
		
		// arr을 순환하며 누적 카운트를 이용하여 각 자리수별 기준으로 sort 배열에 정렬한다.
		for(int i = arr.length-1; i >=0 ; i--) {
			sort[count[(arr[i]/k)%10]-1] = arr[i];
			count[(arr[i]/k)%10]--;
		}
		
		return sort;
	}


	private static void printArray(int[] sort) {
		for(int i = 0; i < sort.length; i++) {
			System.out.print(sort[i] + " ");
		}
		
		System.out.println();
	}
}

//-------------------------------------------//

1자리로 정렬 : 21 11 142 243 13 86 7 
10자리로 정렬 : 7 11 13 21 142 243 86 
100자리로 정렬 : 7 11 13 21 86 142 243 
최종정렬 : 7 11 13 21 86 142 243