감 1도 없는 개발자

감 1도 없는 개발자

여행을 꿈꾸는 개발자

Heap 정렬

Updated:

강의 사이트
  • http://www.kocw.net/home/search/kemView.do?kemId=1148815

Heap 정렬

1. 힙정렬의 개요

  • 최악의 경우 시간복잡도 O(nlog2n)이다.
  • 추가 배열이 필요 없다.
  • 이진 트리 자료구조를 사용.
  • 실제로는 트리를 만들어서 이용하는 것이 아닌 이런 개념을 가져와서 배열을 정렬한다는 의미.

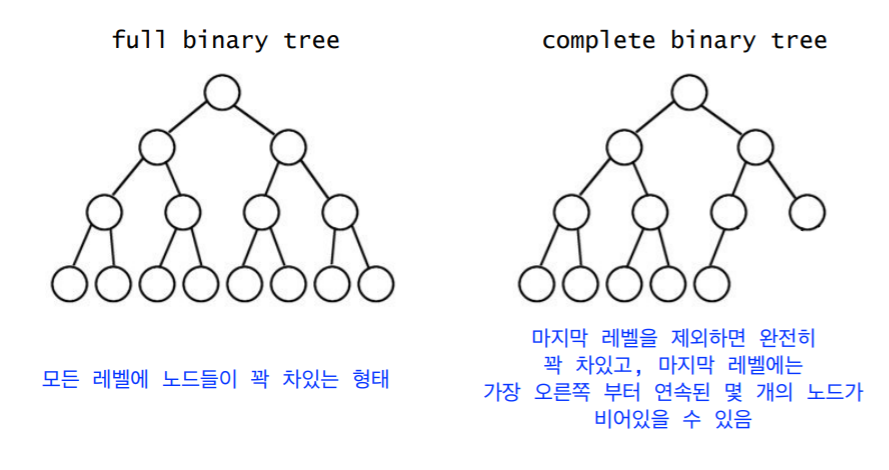
2. Full Binary Tree vs Complete Binary Tree

  • Full Tree 이진 트리는 complete 이진 트리이기도 하다.

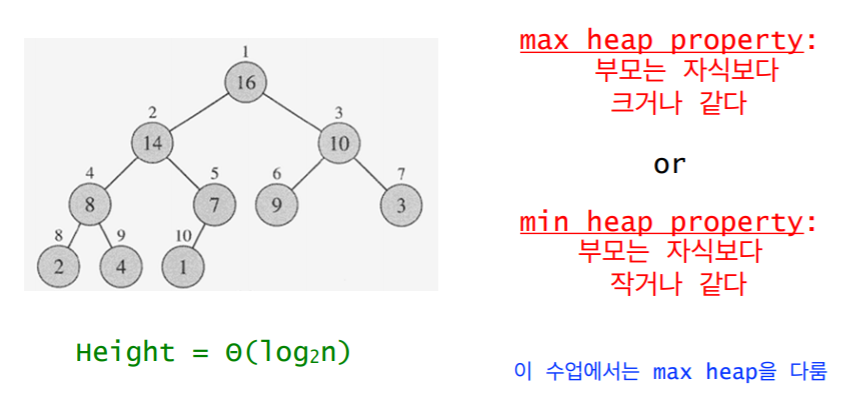
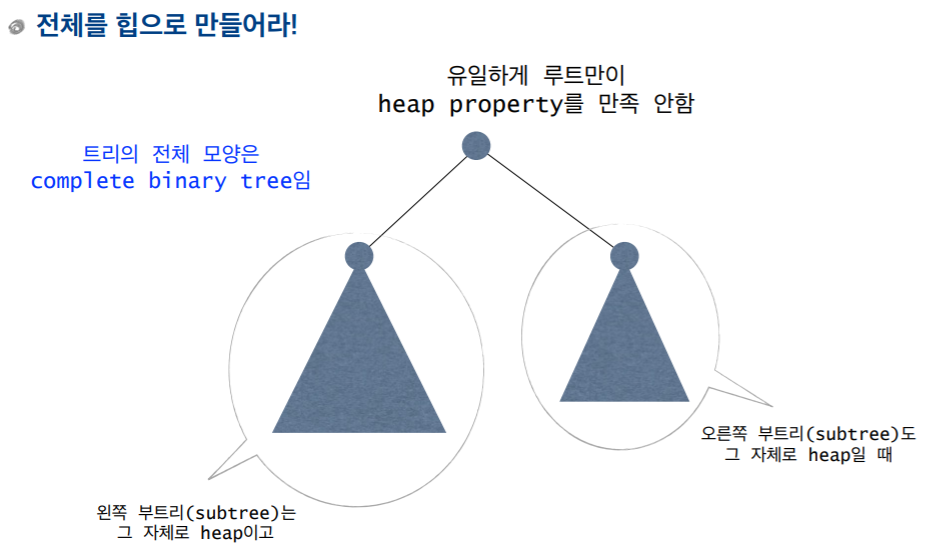
3. Heap의 조건

  1. complete 이진 트리여야한다.

  2. heap property를 만족해야 한다. (Max Heap이냐 Min Heap이냐)

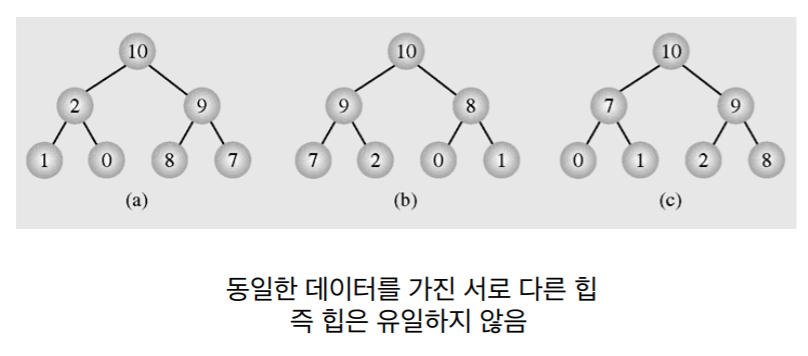
  • 같은 데이터라도 여러 형태의 Heap이 생길 수 있다.

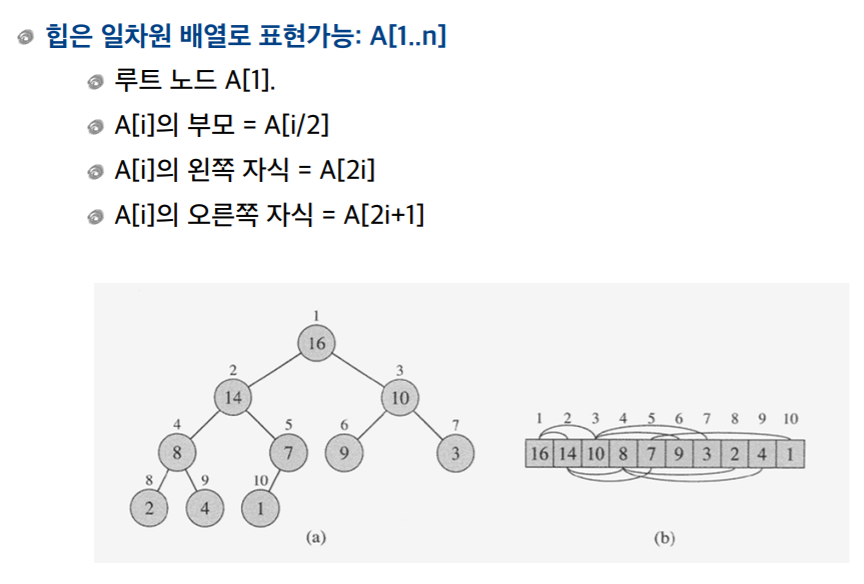
4. Heap을 배열로 표현

  • Heap을 배열로 표현이라기 보다 같은 구조이다라고 보는게 맞을듯

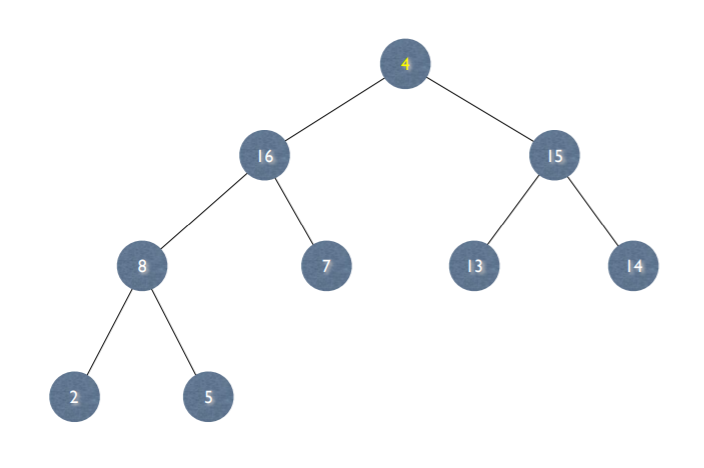
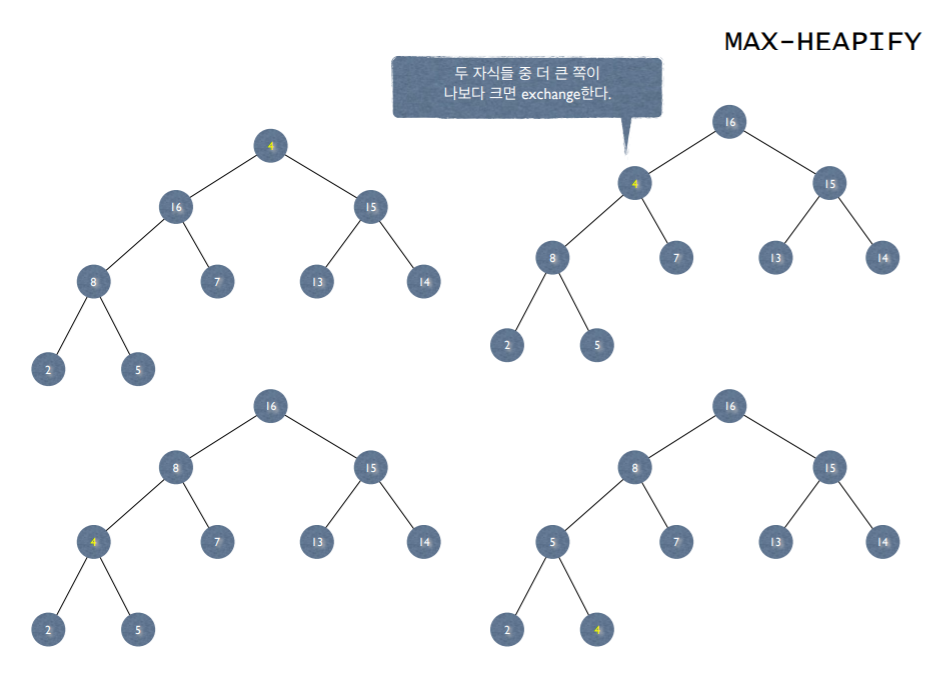
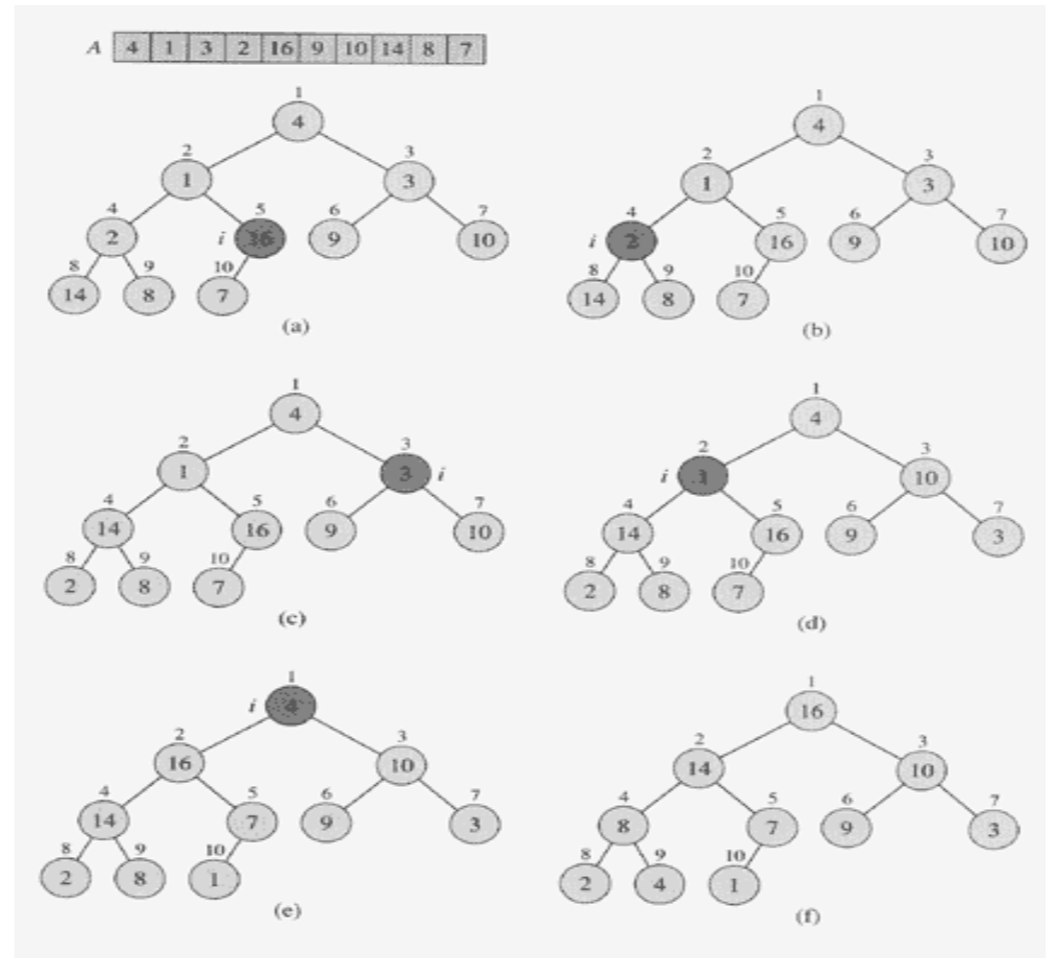
5. Max-Heapify

  • Heapify 과정이 일어나는 그림 예제

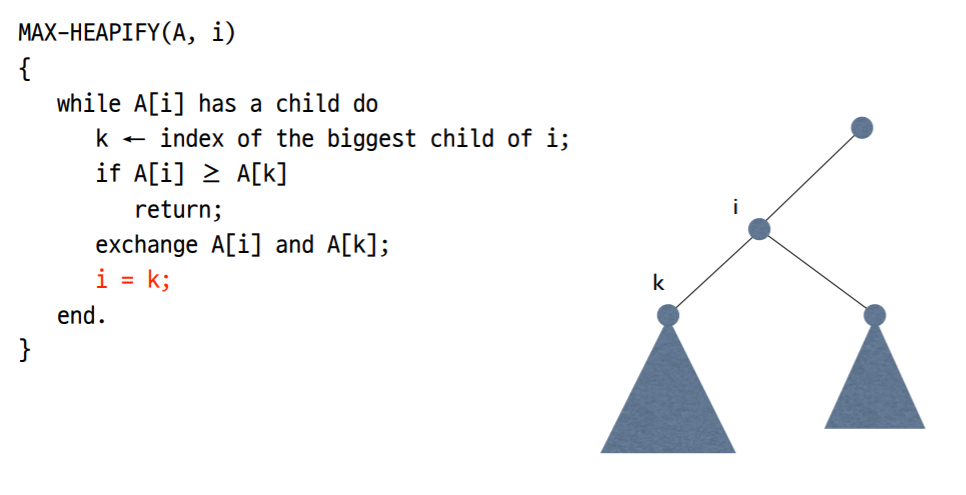
6. Heapify의 Pseudo Code (Recursion)

  • i가 heapify할 노드의 대상

7. Heapify의 Pseudo Code(Iterative)

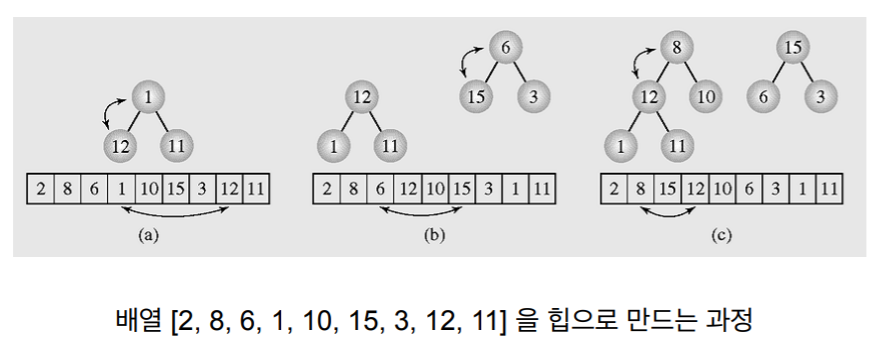
8. 정렬할 배열을 힙으로 만들기

  • N은 배열의 갯수이다.

  • heapify를 시작하는 노드는 N / 2이다.

  • heapify 한번 하는데 걸리는 시간은 logN이다.
  • 1에서 N /2 번까지 반복하기 때문에 총 걸리는 시간은 (n / 2) log N. 즉 O(N logN).
  • 정확하게 말하면 배열을 힙으로 만드는 시간은 O(n)이다.
  • 그러나 Heap sort 만드는 단계는 1. 힙을 만드는 시간. 2. 정렬하는 시간
  • 1.에서 O(n)이지만 2에서 Nlog N이므로 배열을 힙으로 만드는 시간이 O(N)이라고 하지만 힙 정렬을 하는 시간이라고 하면 보통 NlogN이라고 함 (뭔 이야기 인가 함 처음에는 근데 끝까지 보면 이해가 감)

  • 위의 이야기를 모두 아래 그림으로 표현

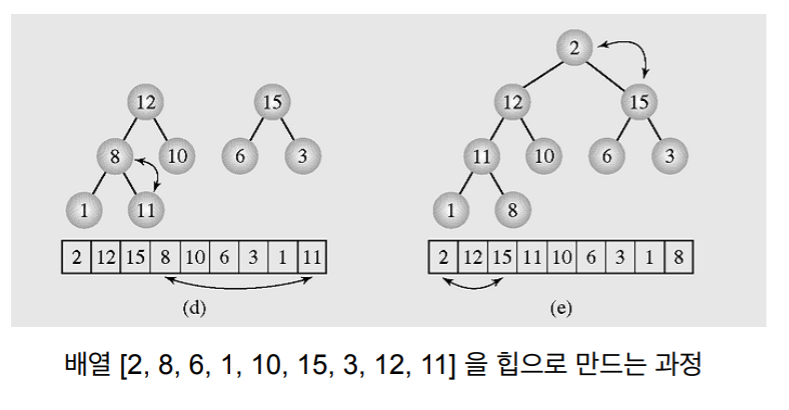
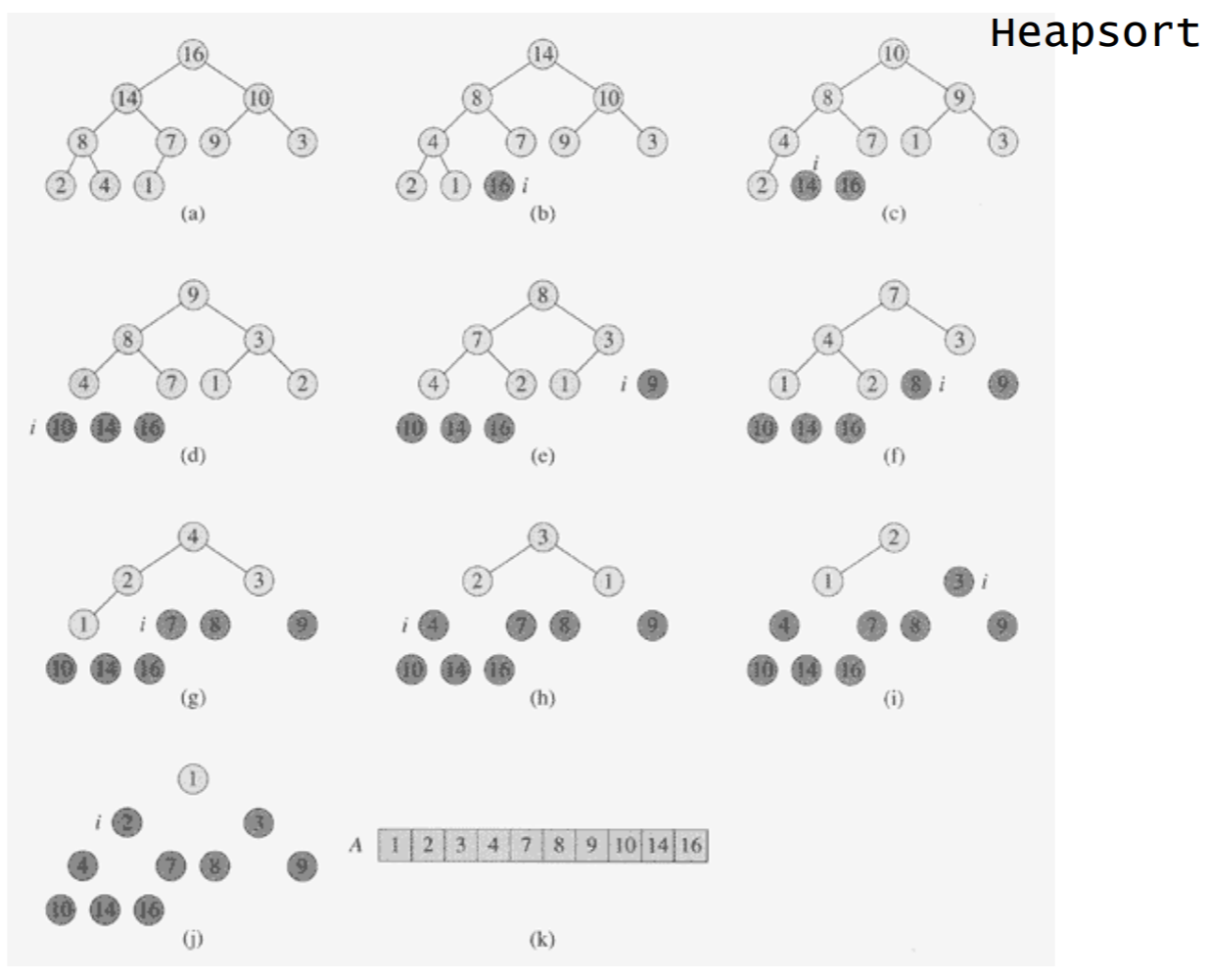
9. 힙 정렬 순서

  1. 주어진 데이터로 힙을 만든다. (8. 정렬할 배열을 힙으로 만들기를 말함. Heapify(N/2)를 한다.)
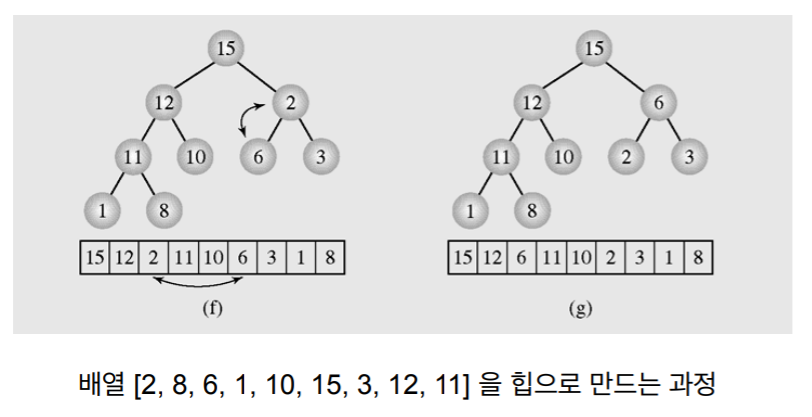
  2. 힙에서 최대값(루트)을 가장 마지막 값과 바꾼다.
  3. 힙의 크기가 1 줄어든 것으로 간주한다. 즉, 가장 마지막 값은 힙의 일부가 아닌 것으로 간주한다.
  4. 루트 노드에 대해서 HEAPIFY(1)한다. (왜냐하면 Heap 되어 있는 상태에서 루트 노드만 바뀌었으니까. 즉 루트 노드 왼쪽 오른쪽으로는 Heap 상태이고 이것만 제자리로 가면 되니까)
  5. 2 ~4 번 반복한다.
  • 위의 이야기를 아래 그림으로 표현

11. 최종 시간 복잡도

  • 최초 HEAP을 만드는데 걸리는 시간 O(n)
  • Heapify 하는데 걸리는 시간 O(log2 N)이므로
  • 평균 걸리는 시간은 O(N log2 N)이다.

12. 구현

public class HeapSort {
	public static void main(String[] args) {
		int[] sort = new int[] {31, 8, 48, 11, 3, 73, 20, 29, 65, 15};
		heapSort(sort);
		printArray(sort);
	}
	
	private static void printArray(int[] sort) {
		for(int i = 0; i < sort.length; i++) {
			System.out.print(sort[i] + " ");
		}
		
		System.out.println();
	}
	
	private static void heapSort(int[] sort) {
		
		//최초로 Max heap을 만듬
		for(int i = sort.length /2 ; i >=0; i--) {
			heapify(sort, sort.length, i);
		}
		
		//첫 번째 인덱스 값을 맨 뒤 배열과 바꾸고
		//바뀐 첫 번째 인덱스를 가지고 heapify 진행
		
		for(int i = sort.length-1; i > 0; i--) {
			swap(sort, 0, i); //항상 맨뒤가 아니라 이전 최대값의 전 인덱스
			heapify(sort, i, 0); 
			// 맨위에서는 sort의 크기를 가운데 인자값으로 넣었으나 여기서 i를 넣은 이유는
			// 당연히 최대 값을 sort 배열 맨뒤로 계속해서 옮겼기 때문에 그걸 뺀 만큼 크기를 비교
			// 하기 위해서 이다.
		}
	}

	private static void heapify(int[] sort, int n, int i) {
		// sort 크기이다. (항상 고정 값이 아니라 최대값을 찾아서 맨뒤로 보낸 경우 그건 제외시켜야
		// 하므로 n도 수시로 바뀐다.
		// i는 내가 heapify 할 배열의 위치
		int parent = i;
		int leftChild = i * 2;
		int rightChild = i * 2 + 1;
		
		//왼쪽 노드가 있고 내가 비교할 노드보다 크다면 일단 leftchild라고 생각해두다가
		if(leftChild < n && sort[parent] < sort[leftChild]) {
			parent = leftChild;
		}
		// 오른쪽 노드가 존재하고 왼쪽 노드보다 크다면 or 왼쪽 노드가 내가 비교할 노드보다 작아서
		// 오른쪽 노드와 부모노드랑 비교했을 때 오른쪽 노드가 크다면 rightchild로 확정
		if(rightChild < n && sort[parent] < sort[rightChild]) {
			parent = rightChild;
		}
		// 그래서 부모노드가 바뀔 예정이라면 실제 바꿔주고
		if(parent != i) {
			swap(sort, parent, i);
			heapify(sort, n, parent);
			//바뀐 부모노드로 이동하여 heapify 해준다.
		}
		
	}

	private static void swap(int[] sort, int parent, int i) {
		int temp = sort[parent];
		sort[parent] = sort[i];
		sort[i] = temp;
	}
}

13. 힙의 응용 : 우선순위 큐

  • 최대 우선순위 큐(maximum priority queue)는 두 가지 연산을 지원하는 자료구조
    • INSERT(x) : 새로운 원소 X를 삽입
    • EXTRACT_MAX() : 최대값을 삭제하고 반환
  • 최소 우선순위 큐는 EXTRACT-MAX 대신 EXTRACT-MIN으로 대체
  • MAX HEAP을 이용하여 최대 우선순위 큐를 구현

13.1 Pseudo Code (Insert)

  • 힙 정렬이 된 배열이라고 가정

  • 1개가 추가 됐으므로 heap 크기(배열의 크기)가 하나 증가
  • 배열의 마지막 위치에 새로 들어올 숫자를 넣음
  • heapify 할 위치는 당연히 새로 들어온 숫자의 위치(즉, 배열의 마지막 위치)
  • 부모노드와 비교하며 올라가기

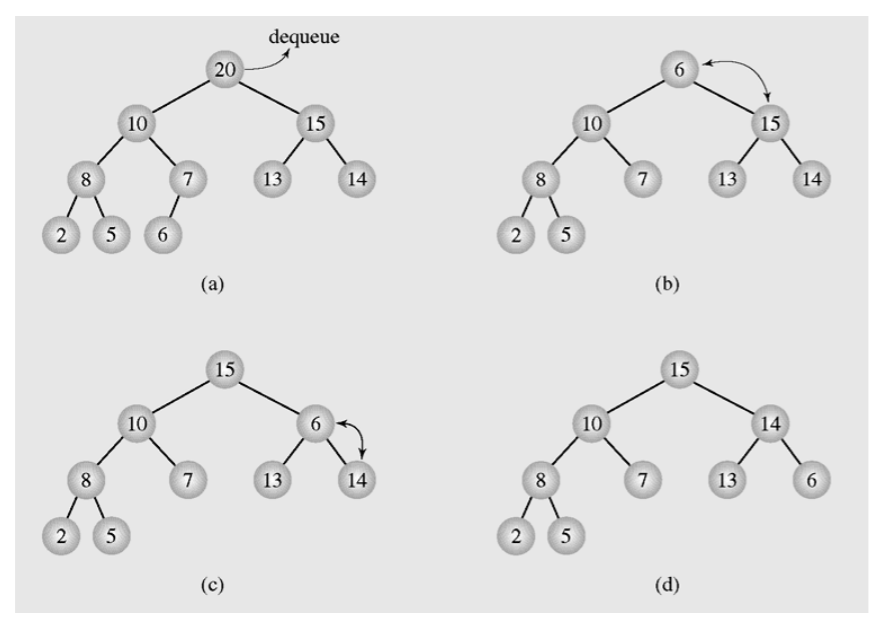
13.2 Pseudo Code (Extract_MAX())

  • 20을 삭제함(반환)
  • 맨 마지막 노드(배열의 끝에 있는 원소)를 루트 노드로 옮김
  • 그리고 HEAPIFY(1) 하면 됨

You may also enjoy