감 1도 없는 개발자

감 1도 없는 개발자

여행을 꿈꾸는 개발자

Quick Sort

Updated:

강의 사이트
  • http://www.kocw.net/home/search/kemView.do?kemId=1148815

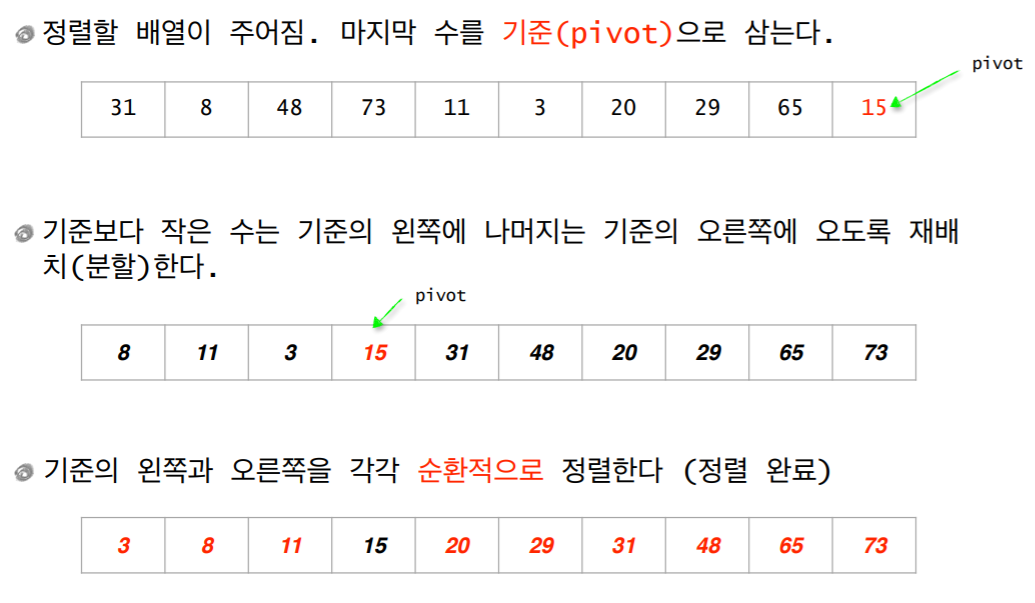
퀵정렬(Quick Sort)

  • 분할, 정복, 합병을 가지고 만든 정렬

1.1 퀵 소트 개념

1.2 퀵소트의 psuedo code

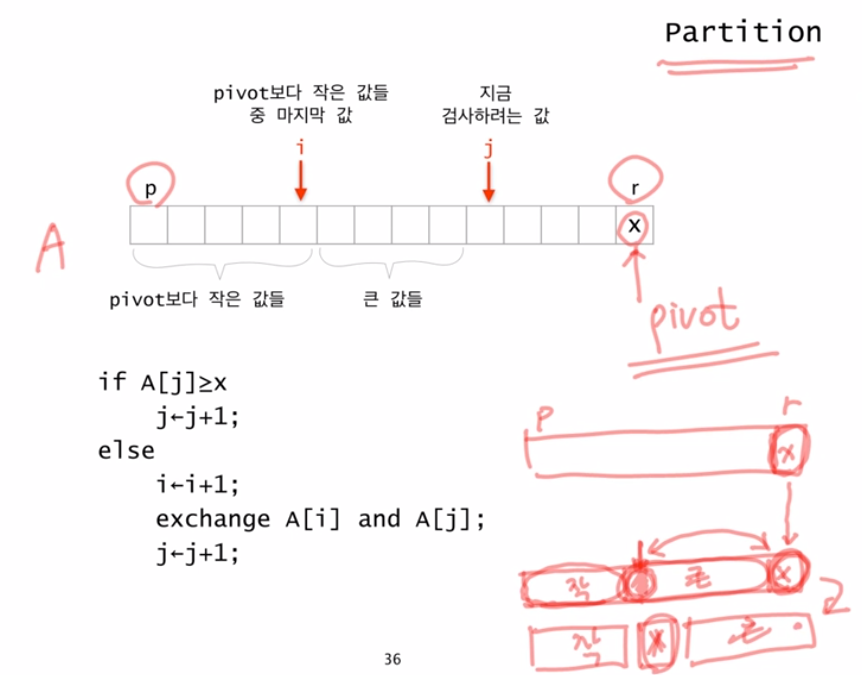
1.3 partition 구현

  • pivot x보다 작은 수들은 왼쪽, 큰 수들은 오른쪽으로 나눈다.
  • 그리고 X보다 큰 수들 중 가장 작은 수의 왼쪽에(다시 말하면 pivot의 위치, 또 다르게 말하면 작은 수들 중 가장 큰 수의 오른쪽) X를 둔다.
  • 그림에서 i는 X보다 작은 수들 중 가장 큰 수의 위치를 가르키고 있다.
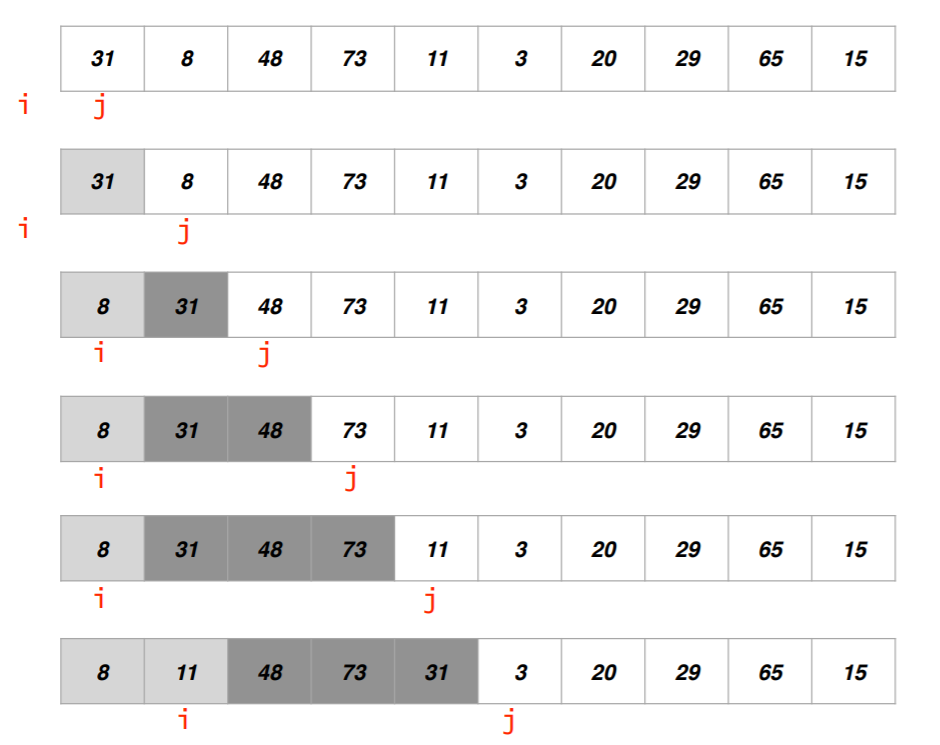
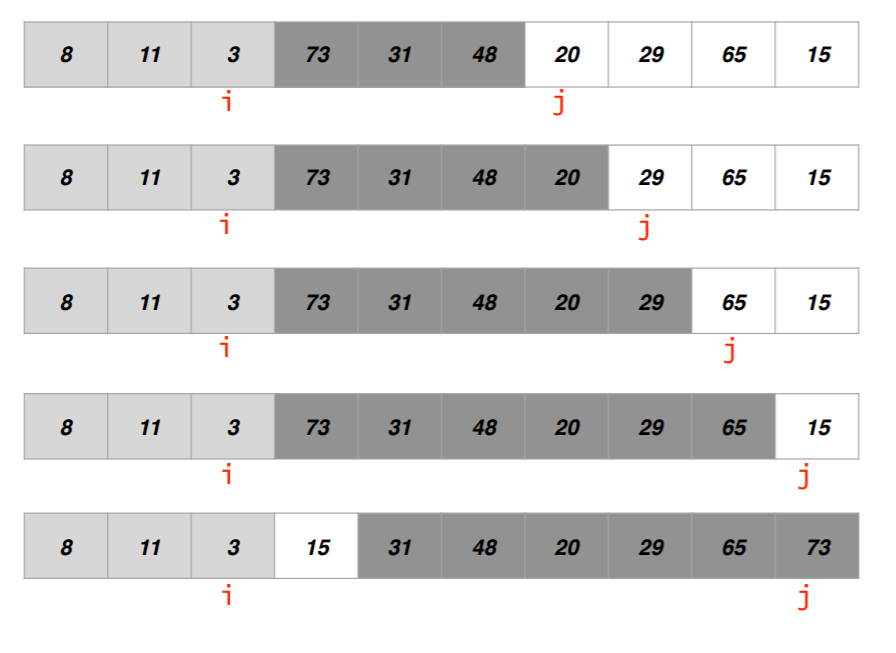
  • 아래는 그림으로 partition의 동작을 보여준다.

1.4 partition psuedo code

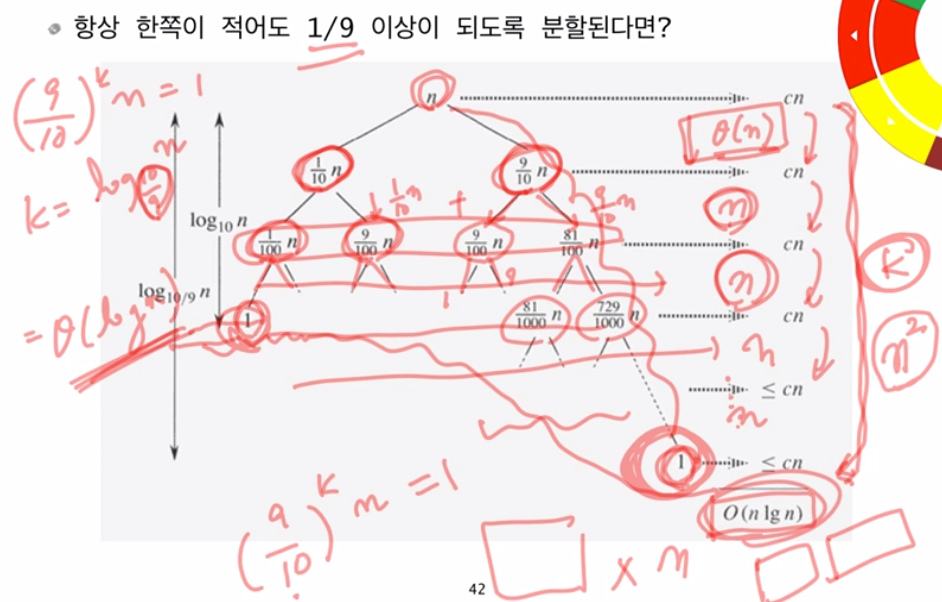
1.5 시간복잡도

  • 머지 소트의 경우 주어진 데이터 상관 없이 똑같이 나누어 분할정복함
  • 퀵소트도 분할 정복을 쓰나 pivot에 따라서 달라짐
  • privot이 주어진 데이터에서 가장 큰 수라고 가정한다면 최악임 (즉, 이미 정렬된 데이터라면 or 거꾸로 정렬)
  • 왜냐하면 pivot을 통해서 주어진 데이터를 비교하여 분할하는데 pivot이 가장 큰 수라면 N의 데이터가 N-1개의 데이터와 pivot으로 분할된다. 그럼 N-1개의 데이터는 또다시 N-1개는 N-2번 반복하여 비교해야 한다. 이런식으로 진행된다면 비교하는 수가 N-1 + N-2 + N-3 +… + 1이므로 점화식을 통해 계산하면 이때 최악의 시간 복잡도는 O(n^2)
  • 따라서 pivot이 가장 가운데로 오는 것이 가장 좋은 경우의 수

  • 이때 최고의 경우의 시간복잡도는 O(nlogn)이다.
  • 그런데 현실적으로 데이터가 주어진다면 이미 정렬된 데이터 같은 건 거의 존재 하지 않는다.
  • 따라서 평균적으로 따지면 퀵소트가 다른 기존의 정렬보다는 상대적(비교적) 좋다라고 할 수 있다.

1.7 평균 시간 복잡도

  • 1부터 N까지 pivot이 될 각 경우에 대해서 running time을 계산
  • 그 running time을 다 더해서 평균시간을 구하면 n Log2N이 나온다.
  • 그림에서 A(n) = n/2로 나오는데 틀림. 2 /n임

1.8 Pivot 선택

  1. 첫 번째 값이나 마지막 값을 피봇으로 선택
  • 이미 정렬된 데이터 or 거꾸로 된 데이터의 경우 최악이 됨
  1. Median(중간 값) of Three
  • 1번을 피하자. 그러나 하필 그 수가 가장 작거나 가장 큰 수일 수 있다. 최악의 시간복잡도를 만날 가능성이 사라지지 않음
  1. 랜덤

  • 평균 시간복잡도를 가짐

  • 내 생각 : 근데 이것도 피할수 없는거 아닌가? 강의에서 말하듯이 악의적인 경우는….

1.9 구현

public class QuickSort {

	public static void main(String[] args) {
		int[] sort = new int[] {31, 8, 48, 73, 11, 3, 20, 29, 65, 15};
		quickSort(sort, 0, sort.length-1);
		printArray(sort);
	}
	
	private static void quickSort(int[] sort, int p, int r) {
		if(p < r) {
			int k = partition(sort, p, r); // pivot값을 기준으로
			quickSort(sort, p, k-1); // 왼쪽 배열을 보내기
			quickSort(sort, k+1, r); // 오른쪽 배열을 보내기
		}
	}

	private static int partition(int[] sort, int p, int r) {

		int i = p;
		
		for(int j = p; j < r; j++) {
			if(sort[r] > sort[j]) { // pivot과 비교하며 작은 수들은 왼쪽으로 몰기
				int temp = sort[i];
				sort[i] = sort[j];
				sort[j] = temp;
				i++; // sort[r], 즉, pivot 값이 들어갈 위치
			}
		}
		
		int temp = sort[i];
		sort[i] = sort[r];
		sort[r] = temp;
		
		printArray(sort);
		
		return i; // pivot값의 위치를 반환
	}

	private static void printArray(int[] sort) {
		for(int i = 0; i < sort.length; i++) {
			System.out.print(sort[i] + " ");
		}
		
		System.out.println();
	}
}

You may also enjoy