Recursion의 개념
Updated:
강의 사이트
- http://www.kocw.net/home/search/kemView.do?kemId=1148815
Recursion의 개념과 기본 예제들
- 순환함수(재귀함수)는 자기 자신을 호출하는 함수
- 무한 루프에 빠질 수 있다. 하지만 올바르게 작성한다면 괜찮다.
- 순환함수는 반복문(interation)으로 변경 가능. 그 역도 성립
- 경우에 따라 반복문보다 간단하게 보일 수 있음
- 적어도 하나의 재귀에 빠지지 않는 경우가 존재해야 한다. 이를 base case라 한다.
- 반복하다보면 결국 base case로 수렴해야하는 조건이 있어야 한다. 이를 recursion case라 한다.
- 팩토리얼 함수 예제
public static void main(String[] argv) {
System.out.println(factorial(10));
}
private static int factorial(int i) {
if(i <= 1) { //base case // 0!=1 이므로 조건을 이렇게
return 1;
}
return i+ factorial(i-1); //recursion case
}
- 최대공약수 예제
public static void main(String[] argv) {
System.out.println(gcd(12, 18));
}
private static int gcd(int i, int j) {
if(j == 0) { // base case
return i;
}
return gcd(j, i % j); // recursion case
}
- 피보나치 예제
public static void main(String[] argv) {
System.out.println(fibonacci(5));
}
private static int fibonacci(int i) {
if(i <=2) {
return i;
}
return fibonacci(i-2) + fibonacci(i-1);
}
- 문자열을 역순으로 출력하는 예제
public static void main(String[] argv) {
reverseString("recursion");
}
private static void reverseString(String string) {
if(string.length() == 0) {
return;
}
reverseString(string.substring(1));
System.out.print(string.charAt(0));
}
- 이진수로 변환 하는 예제
public static void main(String[] argv) {
printBinary(12);
}
private static void printBinary(int i) {
if(i < 2) {
System.out.print(i);
return;
}
printBinary(i / 2);
System.out.print(i % 2);
}
순환적 알고리즘 설계
- 암시적(implicit) 매개변수를 명시적(explicit) 매개변수로 바꿔라
int search(int[] data, int n, int target) {
for(int i = 0; i < n ; i++) {
if(data[i] == target) {
return i;
}
}
return -1;
}
// 검색 구간의 인덱스 0은 부터 시작. 명시적이아닌 즉, 암시적 매개변수이다.
- 위의 코드를 순환함수로 변경
int search(int[] data, int begin, int end, int target) {
if(begin > end) {
return -1;
}
else if(target == data[begin]) {
return begin;
} else {
return search(data, begin+1, end, target);
}
}
// 검색 구간의 시작점을 명시적으로 지정.
// search(data, 0, n-1, target)으로 호출
응용 예제 1: 미로찾기
- 현재 위치에서 출구까지 가는 경로가 있으려면
- 현재 위치가 출구이거나 혹은
- 이웃한 셀들 중 하나에서 현재 위치를 지나지 않고 출구까지 가는 경로가 있거나
- pseudo code
boolean findPath(x,y){
if(x,y) is the exit // 1
return true;
else
mark (x,y) as a visited cell; // 2
for each neighbouring cell (x',y') of (x,y) do // 3
if(x',y') is on the pathWay and not visited// 4
if findPath(x',y') // 5
return true;
return false;
}
- 1 - x,y가 출구이면 true
- 2 - x,y가 이미 접근했던 위치라면 표시
- 3 - x,y에 인접한 cell(경로)들을 순환하는데 (최대 4번)
- 4 - x’,y’가 유효한 cell(경로)이라면 (벽이거나 이미 방문했던 것은 재검사 필요 없음)
-
5 - 4에서 유효하다면 새로운 x’,y’에 대한 검증 findPath 호출
- 이를 더 깔끔하게 변경
boolean findPath(x,y){
if (x,y) is either on the wall or a visited cell
return false;
else if(x,y) is the exit
return true;
else
mark (x,y) as a visited cell;
for each neighbouring cell (x',y') of (x,y) do
if findPath(x',y')
return true;
return false;
}
-
대신 순환 함수가 더 호출됨. 대신 코드가 간결 해짐
-
최종 작성된 코드
public class Maze {
private static int N = 8;
private static int [][] maze = {
{0,0,0,0,0,0,0,1},
{0,1,1,0,1,1,0,1},
{0,0,0,1,0,0,0,1},
{0,1,0,0,1,1,0,0},
{0,1,1,1,0,0,1,1},
{0,1,0,0,0,1,0,1},
{0,0,0,1,0,0,0,1},
{0,1,1,1,0,1,0,0},
};
private static final int PATH_WAY_COLOUR = 0;
private static final int WALL_COLOUR = 1;
private static final int BLOCKED_COLOUR = 2;
private static final int PATH_COLOUR = 3;
public static void main(String[] argv) {
printMaze();
findMazePath(0,0);
System.out.println();
printMaze();
}
public static boolean findMazePath(int x, int y) {
if(x < 0 || y < 0 || x >= N || y >= N) { // 행렬의 크기 8을 넘었을 경우
return false;
} else if(maze[x][y] != PATH_WAY_COLOUR) { //이미 방분했거나 벽인 경우
return false;
} else if(x == N-1 && y == N-1) { // maze[7][7]. 즉 출구이면 true
maze[x][y] = PATH_COLOUR;
return true;
} else {
maze[x][y] = PATH_COLOUR; // 위에 조건을 통과했다는 것은 유효한 셀에 도착
if(findMazePath(x-1, y) || findMazePath(x, y+1)
|| findMazePath(x+1, y) || findMazePath(x, y-1)) {
return true;
} // 그 다음 인접한 방향(위치, 셀)에 대한 유효성 검사
maze[x][y] = BLOCKED_COLOUR;
return false;
}
}
private static void printMaze() {
for(int i = 0 ; i < N ; i++) {
for(int j = 0 ; j < N; j++) {
System.out.print(maze[i][j]);
}
System.out.println();
}
}
}
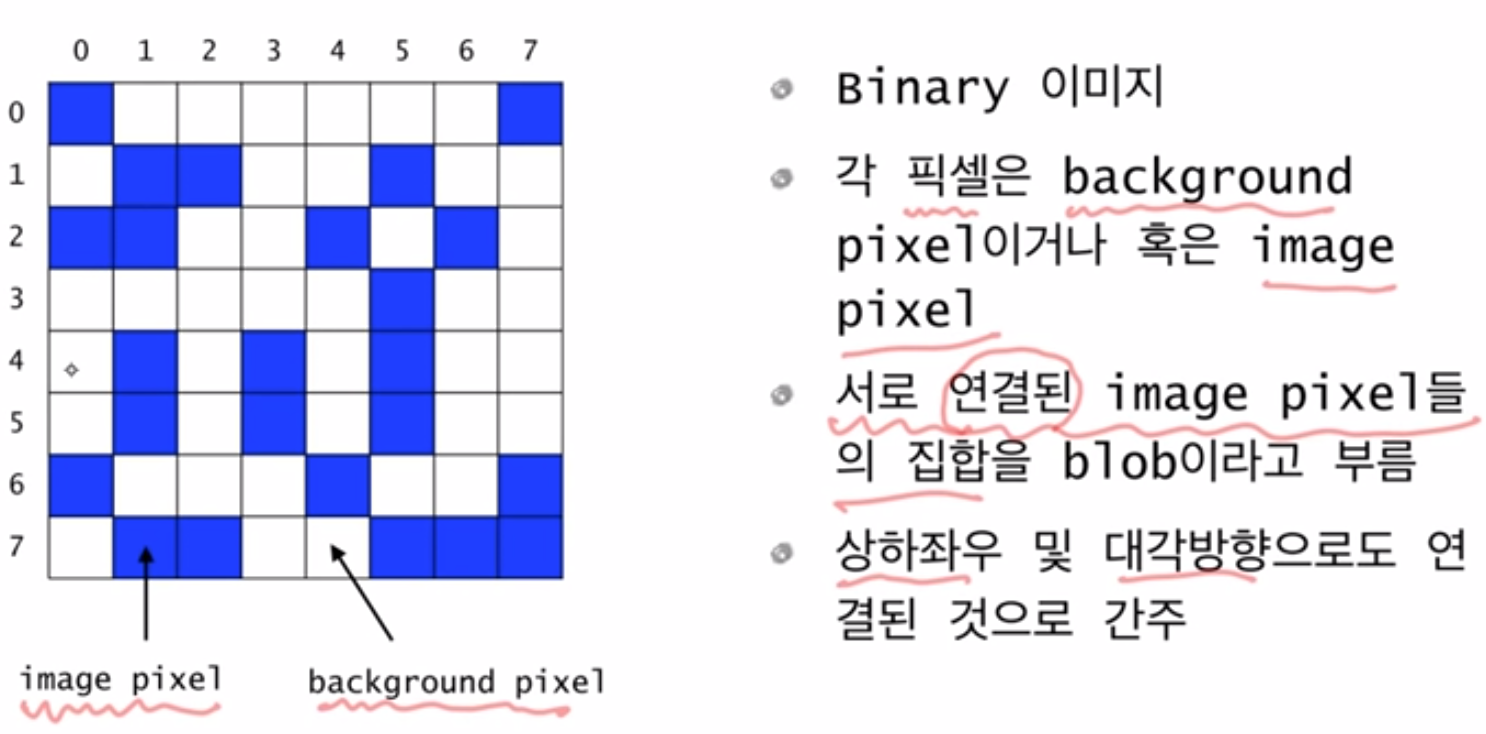
응용예제 2 : Counting Cells in a Blob
-
현재 픽셀이 속한 blob의 크기를 카운트하려면
-
현재 픽셀이 image color가 아니라면
0을 반환한다
-
현재 픽셀이 image color라면
먼저 현재 픽셀을 카운트 한다 (count =1)
현재 픽셀에 중복 카운트되는 것을 방지하기 위해 다른 색으로 칠한다.
현재 픽셀에 이웃한 모든 픽셀들에 대해서 그 픽셀이 속한 blob의 크기를 카운트하여 카운터 더 해준다.
카운터를 반환한다.
-
-
수도 코드
if the pixel(x,y) is outside the grid
the result is 0;
else if pixel(x,y) is not an image pixel or already counted
the result is 0;
else
set the color of the pixel (x,y) to a red color;
the result is 1 plus the number of cells in each piece of the blob that includes a nearest neighbour;
- 실제 코드
public class CountingBlob {
private static int N = 8;
private static int [][] blob = {
{1,0,0,0,0,0,0,1},
{0,1,1,0,0,1,0,0},
{1,1,0,0,1,0,1,0},
{0,0,0,0,0,1,0,0},
{0,1,0,1,0,1,0,0},
{0,1,0,1,0,1,0,0},
{1,0,0,0,1,0,0,1},
{0,1,1,0,0,1,1,1},
};
private static final int BACKGROUND_COLOUR = 0;
private static final int IMAGE_COLOUR = 1;
private static final int ALREADY_COUNT = 2;
public static void main(String[] argv) {
System.out.println(countCells(4, 3));
}
public static int countCells(int x, int y) {
if(x < 0 || y < 0 || x >= N || y >= N) {
return 0;
} else if(blob[x][y] != IMAGE_COLOUR) {
return 0;
} else {
blob[x][y] = ALREADY_COUNT;
return 1 + countCells(x-1,y+1) + countCells(x,y+1)
+ countCells(x+1,y+1) + countCells(x-1,y)
+ countCells(x+1,y) + countCells(x-1,y-1)
+ countCells(x,y-1) + countCells(x+1,y-1);
}
}
}
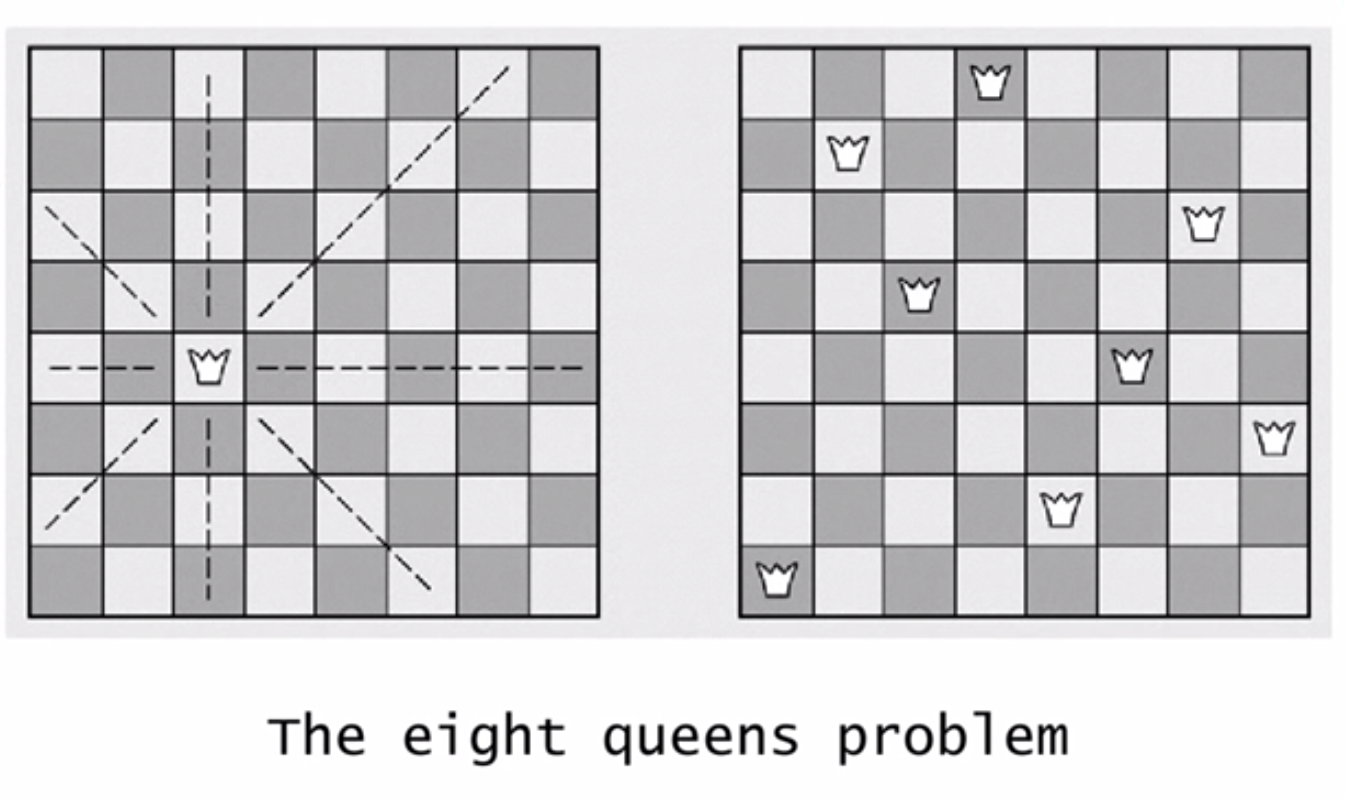
응용예제 3 : N Queens
- 한 줄에 하나의 퀸이 꼭 놓어야 한다면 어디에 놓여야 하는가?
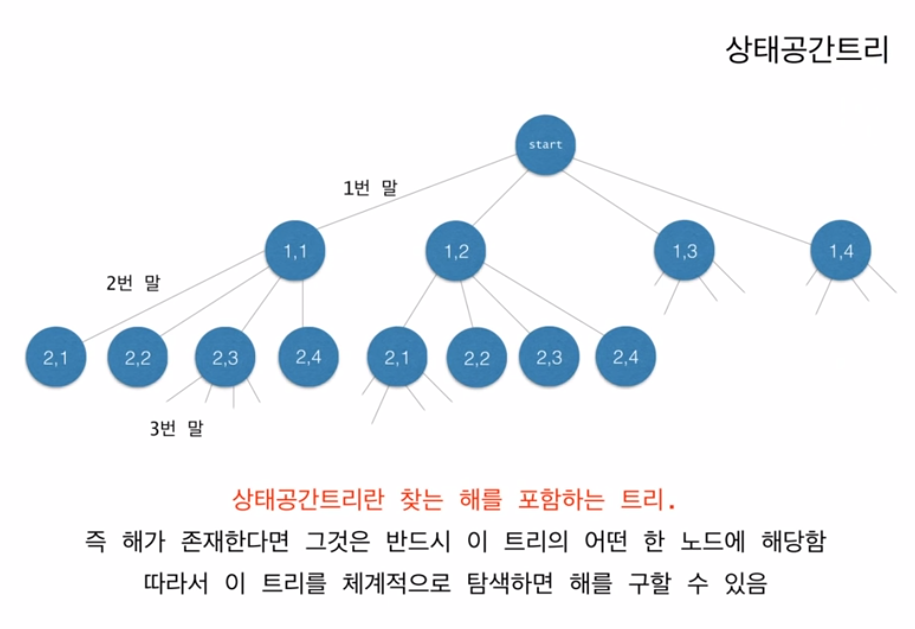
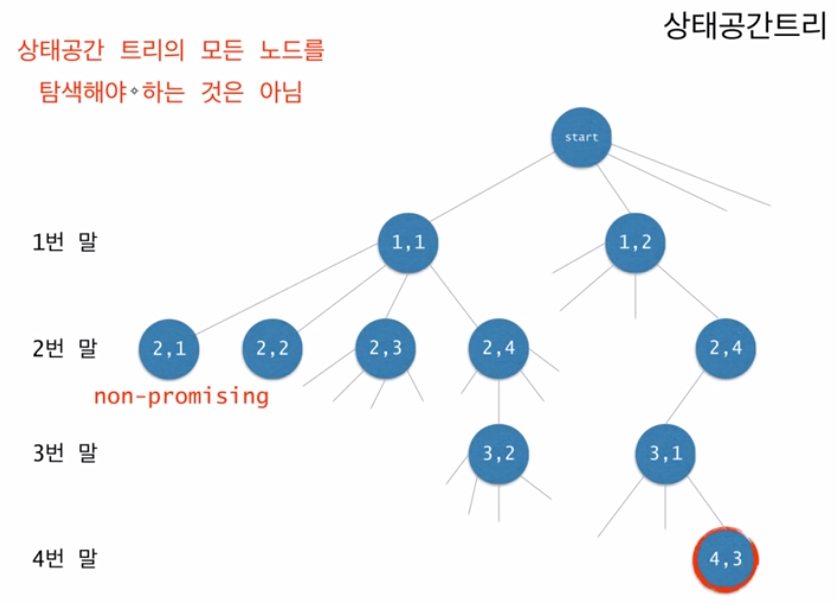
- 상태공간 트리를 깊이 우선 방식으로 탐색(되추적 기법: Backtracking)하여 해를 찾는 알고리즘
- 수도코드
//N은 배열 크기
//cols는 각 행에 놓일 퀸의 위치를 저장하는 변수
//예를 들어 1행에 1, 2행에 4 3행에 2에 놓였다면 cols에는 1,4,2 이렇게 들어가 있다.
int[] cols = new int [N+1]; // 전역변수
boolean queens(arguments: int level){
if (!promising(level)) // 도착한 노드가 성공했냐?
return false;
else if (level==N) // 위에 promising을 성공 (최종 4번째 행(N)까지 도착한 성공이냐?)
//출력 메소드 만들면됨 이때
return true;
else // 꽝도 아니고 답도 아니면 자식 노드로 내려 간다.
for(int i = 1; i <=N; i++){
clos[level+1] = i; // 해당 행에서 오른쪽 열로 하나씩 이동하면서
if(queens(level+1)){ // 해당 행의 아래 행들이 성공이냐?
return true;
}
}
return false;
}
- arguments는 어떤 노드에 도착했는지? 즉, 도착한 행의 깊이
- promising 함수는 어떻게 구성해야 하는건가?
- 같은 열에 놓여 있는가? 같은 대각선에 놓였는가?
boolean promising(int level){
for(int i = 1; i < level; i++){
if(cols[i] == cols[level]) // 같은 열에 있는가? 수도 코드에서 cols의 배열에 각 열을 넣 어 놨기 때문에 (clos[level+1] = i;) 그 값으로 비교한다.
return false;
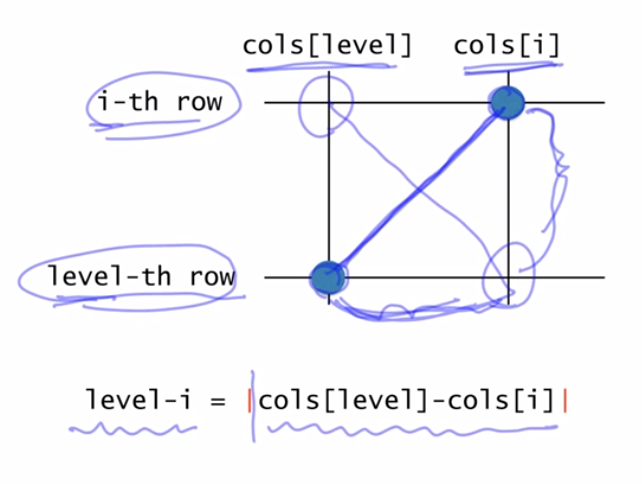
if(level -i == Math.abs(cols[level] - cols[i])) // 같은 대각선에 있는가?
return false;
}
return true;
}
- 대각선의 경우 위의 공식
- 같은 대각선이다라는 것은 행과 열의 차이가 같다라는 것이다. ex) (3,3)과 (1,1)은 같은 대각선
- level-i는 깊이(행)를 나타낸다.
- cols[level] - cols[i]는 대각선의 길이(열)을 나타낸다.
- 그래서 이 둘의 크기가 같다면 같은 대각선에 있는 것
- 절댓값을 붙여준 것은 반대의 방향도 적용
최종 코드
public class NQueens {
static final int N = 4;
static int[] cols = new int[N+1];
private static int [][] board = {
{0,0,0,0},
{0,0,0,0},
{0,0,0,0},
{0,0,0,0}
};
// private static int [][] board = {
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0},
// {0,0,0,0,0,0,0,0,0,0}
// };
public static void main(String[] args) {
System.out.println(nQueen(0));
for(int i = 0; i < N; i++) {
System.out.println(i);
board[i][cols[i+1]-1] = 1;
}
for(int i = 0; i < N; i++) {
for(int j = 0; j < N ; j++) {
System.out.print(board[i][j]);
}
System.out.println();
}
}
private static boolean nQueen(int level) {
if(!isCorrect(level)) {
return false;
} else if(level == N) {
return true;
} else {
for(int i = 1; i <= N; i++) {
cols[level+1] = i;
if(nQueen(level+1)) {
return true;
}
}
return false;
}
}
private static boolean isCorrect(int level) {
for(int i = 1; i < level; i++) {
if(cols[level] == cols[i]) { // 열이 같은가
return false;
}
if(level-i == Math.abs(cols[level] - cols[i])) { // 대각선이 같은가
return false;
}
}
return true;
}
}